
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 5:
Vì \(\frac{x}{10}=\frac{y}{15}=\frac{z}{12}\)\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{12}=\frac{x-y+z}{10-15+12}=-\frac{49}{7}=-7\)
\(\Rightarrow x=-7.10=-70;y=-7.15=-105;z=-7.12=-84\)
Vậy x = -70; y = -105; z = -84
Bài 6:
Ta có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)\(\Rightarrow\frac{x^2}{2^2}=\frac{y^2}{3^2}=\frac{z^2}{4^2}=\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}\)
\(\Rightarrow\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}=\frac{2.z^2}{2.16}=\frac{2z^2}{32}=\frac{x^2-y^2+2z^2}{4-9+32}=\frac{108}{27}=4\)
\(\Rightarrow x^2=4.4=16\Rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)
\(y^2=9.4=36\Rightarrow\orbr{\begin{cases}y=6\\y=-6\end{cases}}\)
\(z^2=4.16=64\Rightarrow\orbr{\begin{cases}z=8\\z=-8\end{cases}}\)
Vậy x = 4; y = 6; z = 8 hoặc x = -4; y = -6; z = -8.
6, TA CÓ :
\(\frac{x^2}{4}\) =\(\frac{y^2}{9}\)=\(\frac{2z^2}{32}\)và x2 -y2 + 2z2 =108
ÁP DỤNG TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU :
TA CÓ :\(\frac{x^2}{4}\) - \(\frac{y^2}{9}\)+ \(\frac{2z^2}{32}\)=\(\frac{x^2-y^2+2z^2}{4-9+32}\)=\(\frac{108}{27}=4\)
=> \(x^2=4.4=16\)=> x = \(\sqrt{16}=4\)
\(y^2=9.4=36\Rightarrow y=\sqrt{36}=6\)
\(2z^2=32.4=128\Rightarrow z^2=\frac{128}{2}=64\Rightarrow z=\sqrt{64}=8\)

\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)
=\(\dfrac{3}{1.4}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)
=\(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}-\dfrac{1}{100}\)
=\(1-\dfrac{1}{100}=\dfrac{99}{100}\)
Mà \(\dfrac{99}{100}< 1\) nên \(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}< 1\)

Bài 7:
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: AB=AE
DB=DE(ΔABD=ΔAED)
=>AD là trung trực của BE
c: Xét ΔDBK và ΔDEC có
góc DBK=góc DEC
DB=DE
góc BDK=góc EDC
=>ΔDBK=ΔDEC
d: ΔDBK=ΔDEC
=>BK=EC
AK=AB+BK
AC=AE+EC
mà AB=AE; BK=EC
nên AK=AC
=>ΔAKC cân tai A
e: AK=AC
DK=DC
=>AD là trung trực của KC
=>AD vuông góc KC


 G
G
 Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!
Mọi người giúp mình giải tiếp bài 5 và bài 6 với!!! Mình đang cần gấp. Thank you !!!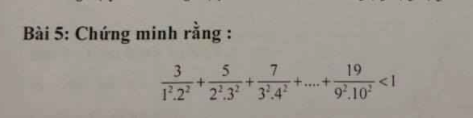 đang cần gấp bài 5 ai giúp mình với ạ :))
đang cần gấp bài 5 ai giúp mình với ạ :))


 Các bạn giúp mình làm bài 5 (câu 4) với ! Mình đang cần gấp . Cho mình cám ơn trước
Các bạn giúp mình làm bài 5 (câu 4) với ! Mình đang cần gấp . Cho mình cám ơn trước
Bài 5:
a) Xét tam giác \(ABD\)và tam giác \(AHD\)có:
\(AH=AB\)(giả thiết)
\(\widehat{BAD}=\widehat{HAD}\)(vì \(AD\)là tia phân giác của góc \(BAH\))
\(AH\)cạnh chung
Suy ra \(\Delta ABD=\Delta AHD\left(c.g.c\right)\)
b) \(\Delta ABD=\Delta AHD\Rightarrow\widehat{AHD}=\widehat{ABD}=90^o\)
do đó \(DH\)vuông góc với \(AC\).
Bài 6:
Xét tam giác \(OAD\)và tam giác \(OBD\)có:
\(OA=OB\)(giả thiết)
\(\widehat{AOD}=\widehat{BOD}\)(vì \(OD\)là tia phân giác góc \(AOB\))
\(OD\)cạnh chung
Suy ra \(\Delta OAD=\Delta OBD\left(c.g.c\right)\)
\(\Rightarrow DA=DB\)(hai cạnh tương ứng)
\(\widehat{ODA}=\widehat{ODB}\)(hai góc tương ứng)
mà \(\widehat{ODA}+\widehat{ODB}=180^o\)(hai góc kề bù)
nên \(\widehat{ODA}=\widehat{ODB}=90^o\)
suy ra \(OD\)vuông góc với \(AB\).