Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

55.
\(3c^2\ge b^2+b^2+a^2\ge\dfrac{1}{3}\left(b+b+a\right)^2=\dfrac{1}{3}\left(2b+a\right)^2\)
\(\Rightarrow9c^2\ge\left(2b+a\right)^2\Rightarrow3c\ge2b+a\)
Do đó:
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\ge\dfrac{9}{3c}=\dfrac{3}{c}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
56.
\(\dfrac{x^2\left(y+z\right)}{yz}\ge\dfrac{4x^2\left(y+z\right)}{\left(y+z\right)^2}=\dfrac{4x^2}{y+z}\)
Tương tự:
\(\dfrac{y^2\left(z+x\right)}{zx}\ge\dfrac{4y^2}{z+x}\) ; \(\dfrac{z^2\left(x+y\right)}{xy}\ge\dfrac{4z^2}{x+y}\)
Cộng vế với vế:
\(P\ge\dfrac{4x^2}{y+z}+\dfrac{4y^2}{z+x}+\dfrac{4z^2}{x+y}\ge\dfrac{4\left(x+y+z\right)^2}{2\left(x+y+z\right)}=2\left(x+y+z\right)=2\)
Vậy \(P_{min}=2\) khi \(x=y=z=\dfrac{1}{3}\)

a: Thay x=-4 vào B, ta được:
\(B=\dfrac{1-2\cdot\left(-4\right)}{2-\left(-4\right)}=\dfrac{1+8}{2+4}=\dfrac{9}{6}=\dfrac{3}{2}\)

Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

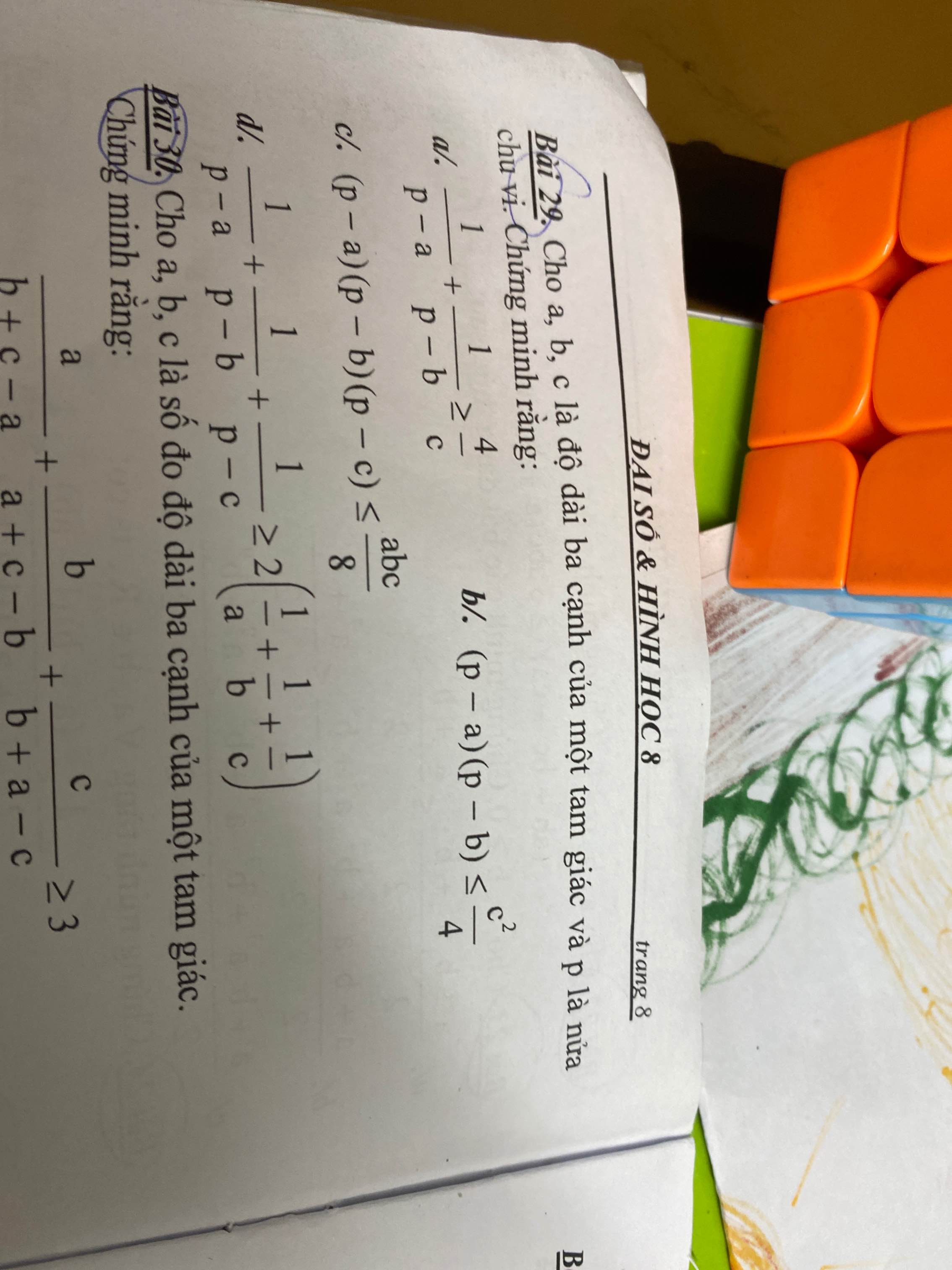







giúp mình với mn ơi