
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
5x + 1 - ( 5x - x2 )
= 5x + 1 - 5x + x2
= x2 + 1
vì x2 \(\ge\)0 nên x2 + 1 > 0
Vậy đa thức trên không có nghiệm

cái này trong SGK thì tra google thì nhanh hơn đó bạn *ý kiến riêng*
Chúc bạn học tốt! :3

10C
14 Cả 4 đáp án sai, đa thức này bậc 6 (mặc dù \(x^6-x^6\) rút gọn mất nhưng vẫn còn 1 hạng tử \(-xy^5\) bậc 6 nên đa thức đã cho có bậc 6)

a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)


Vì a,b,c tỉ lệ nghịch với \(\frac{1}{2};\frac{1}{5};\frac{1}{7}\) nên ta có: \(a.\frac{1}{2}=b.\frac{1}{5}=c.\frac{1}{7}\) hay \(\frac{a}{2}=\frac{b}{5}=\frac{c}{7}\) và a + b - 2c = 70
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{5}=\frac{c}{7}\) \(=\frac{a}{2}=\frac{b}{5}=\frac{2c}{14}=\frac{a+b-2c}{2+5-14}=\frac{70}{-7}=-10\)
\(\Rightarrow\left[\begin{array}{nghiempt}a=-10.2\\b=-10.5\\c=-10.7\end{array}\right.\) \(\Rightarrow\left[\begin{array}{nghiempt}a=-20\\b=-50\\c=-70\end{array}\right.\)
\(\Rightarrow\) \(a+b-c=-20+\left(-50\right)-\left(-70\right)=0\)
Vậy...............

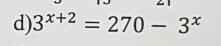
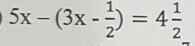


 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp



d:Ta có: \(3^{x+2}=270-3^x\)
\(\Leftrightarrow10\cdot3^x=270\)
\(\Leftrightarrow x=3\)
e: Ta có: \(5x-\left(3x-\dfrac{1}{2}\right)=4\dfrac{1}{2}\)
\(\Leftrightarrow2x+\dfrac{1}{2}=\dfrac{9}{2}\)
hay x=4