Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





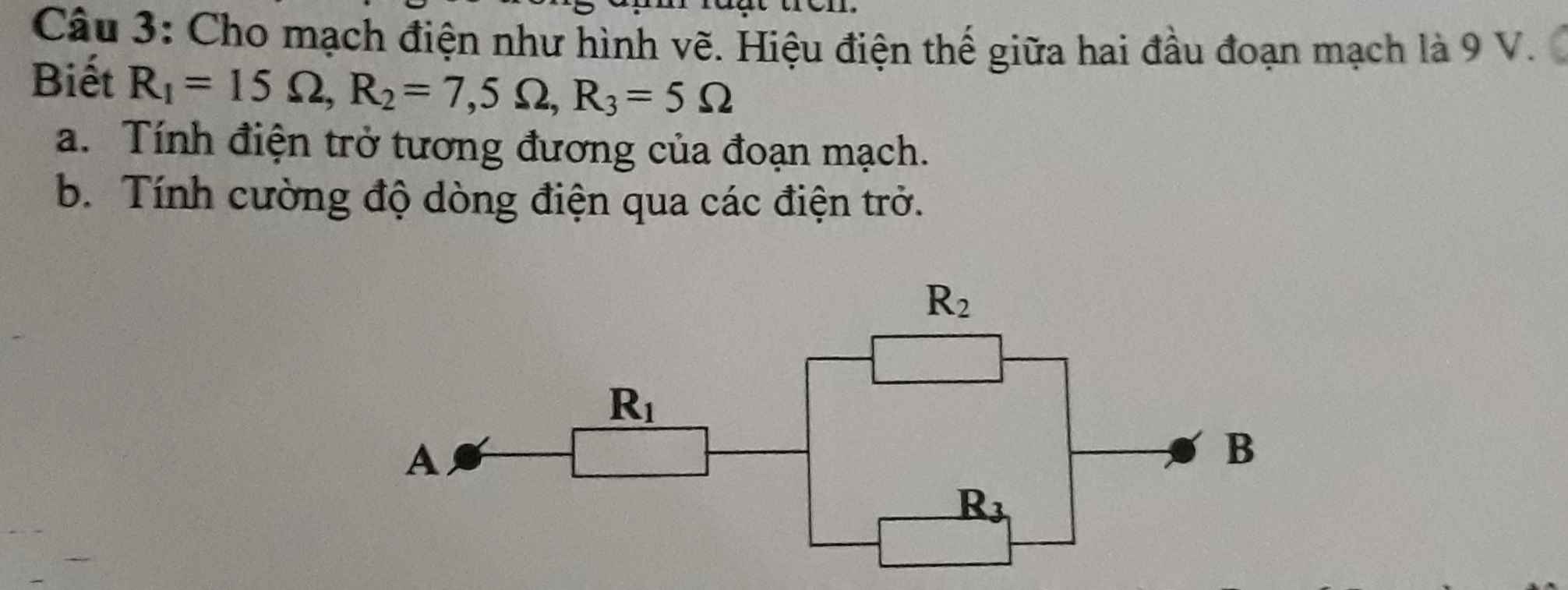
\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{7,5.5}{7,5+5}=3\left(\Omega\right)\)
Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=R_1+R_{23}=15+3=18\left(\Omega\right)\)
Do mắc nối tiếp nên \(I=I_1=I_{23}=\dfrac{U}{R_{tđ}}=\dfrac{18}{9}=2\left(A\right)\)
Do mắc song song nên \(U_{23}=U_2=U_3=I_{23}.R_{23}=2.3=6\left(V\right)\)
\(\left\{{}\begin{matrix}I_2=\dfrac{U_2}{R_2}=\dfrac{6}{7,5}=0,8\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{6}{5}=1,2\left(A\right)\end{matrix}\right.\)

Bạn tự làm tóm tắt nhé!
Bài 1:
a. Ý nghĩa:
Điện trở định mức của biến trở con chạy là 100\(\Omega\)
Cường độ dòng điện định mức của biến trở con chạy là 2A.
b. Hiệu điện thế lớn nhất được phép đặt lên hai đầu dây cố định của biến trở: \(U=R.I=100.2=200V\)
c. Tiết diện của dây dẫn dùng làm biến trở: \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,1.10^{-6}.75}{100}=8,25.10^{-7}m^2\)

\(R_{tđ}=R_1+R_2=100+80=180\Omega\)
\(I_1=I_2=I=\dfrac{U}{R}=\dfrac{210}{180}=\dfrac{7}{6}A\)
Chiều dài 1 vòng quấn:
\(C=\pi\cdot d=0,25\pi\left(m\right)\)
Chiều dài dây dẫn:
\(l=n\cdot C=120\cdot0,25\pi=94,25m\)
Tiết diện dây:
\(S=\rho\dfrac{l}{R_2}=0,5\cdot10^{-6}\cdot\dfrac{94,25}{80}=5,89\cdot10^{-7}m^2\)
a) vì R1 mắc nối tiếp với R2
=> Rtđ=R1+R2=100+80=180 (Ω)
b) cường độ dòng điện qua mỗi điện trở và mạch chính là :
I=I1=I2=U/Rtđ=240/180=4/3 (A)
c) chiều dài 1 vòng quấn là :
l1=3,14.0,025=0,0785m
chiều dài dây dẫn là
l=120.0,0785=9,42 vòng
tiết diện của dây dẫn là
R=p. l/S => S= l.p/R =0,5.10^-6 .9,42/80=5,89.10^-8 m^2


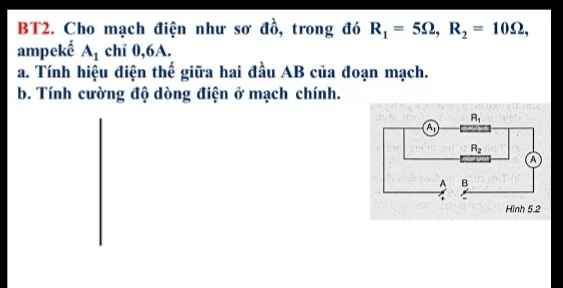
a, HĐT giữa 2 đầu R1:
Ta có: \(I_1=\dfrac{U_1}{R_1}\Leftrightarrow U_1=I_1R_1=0,6.5=3\left(V\right)\)
Mà UAB=U1=U2=3V
b, Điện trở tương đương:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{5.10}{5+10}=3,33\left(\Omega\right)\)
CĐDĐ ở mạch chính:
\(I_{AB}=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{3}{3,33}=0,9\left(A\right)\)


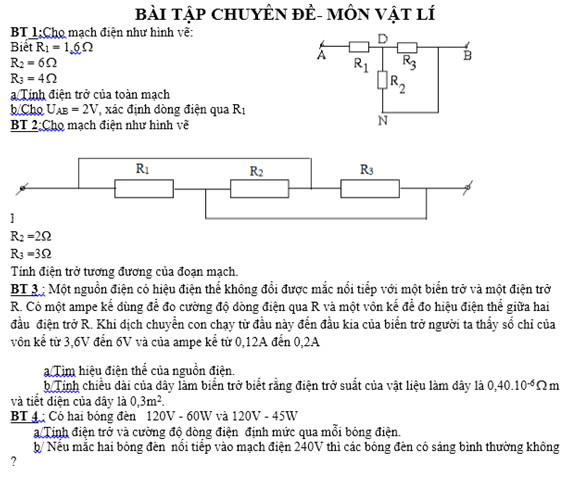 mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.