K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 7 2015
Hình vẽ:
Bài này: bạn cần vẽ 2 đường thẳng xx' và zz' trước sao cho góc xAz = 115o
Tiếp theo, dựa vào điều kiện: góc BAx' = ABy ta vẽ được đường thẳng By (By chính là đường yy', do B là giao của yy' và zz')
b) Ta có: góc ABy = BAx' mà 2 góc này ở vị trí so le trong nên đường thẳng xx' // yy'
=> góc xAB và ABy bù nhau (cặp góc trong cùng phía)
và góc x'AB và ABy' bù nhau (cặp góc trong cùng phía)
28 tháng 6 2021
Câu 9:
d) Xét ΔABC có
AH là đường trung tuyến ứng với cạnh BC
BD là đường trung tuyến ứng với cạnh AC
AH cắt BD tại G
Do đó: G là trọng tâm của ΔABC(đpcm)
LP
2
20 tháng 8 2021
Bài 3:
a: Ta có: \(A=\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-6x^2-33x+10x+55\)
=76
b: Ta có: \(B=\left(x-3\right)\left(x+2\right)-\left(x-5\right)\left(x+4\right)\)
\(=x^2+2x-3x-6-x^2-4x+5x+20\)
=14
25 tháng 12 2021
a: Xét ΔAOM và ΔBOM có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
OA=OB
Do đó: ΔAOM=ΔBOM
NC
31 tháng 8 2020
Bài làm:
Ta có: \(\frac{a}{b}=\frac{c}{d}\Leftrightarrow\frac{a^2}{b^2}=\frac{c^2}{d^2}\Leftrightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Áp dụng t/c dãy tỉ số bằng nhau:
Ta có: \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}=\frac{a^2-b^2}{c^2-d^2}\)
=> \(\frac{a^2+b^2}{a^2-b^2}=\frac{c^2+d^2}{c^2-d^2}\)
31 tháng 8 2020
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\hept{\begin{cases}a=kb\\c=kd\end{cases}}\)
=>\(\frac{a^2+b^2}{a^2-b^2}=\frac{\left(kb\right)^2+b^2}{\left(kb\right)^2-b^2}=\frac{k^2b^2+b^2}{k^2b^2-b^2}=\frac{b^2\left(k^2+1\right)}{b^2\left(k^2-1\right)}=\frac{k^2+1}{k^2-1}\)(1)
=> \(\frac{c^2+d^2}{c^2-d^2}=\frac{\left(kd\right)^2+d^2}{\left(kd\right)^2-d^2}=\frac{k^2d^2+d^2}{k^2d^2-d^2}=\frac{d^2\left(k^2+1\right)}{d^2\left(k^2-1\right)}=\frac{k^2+1}{k^2-1}\)(2)
Từ (1) và (2) => đpcm
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
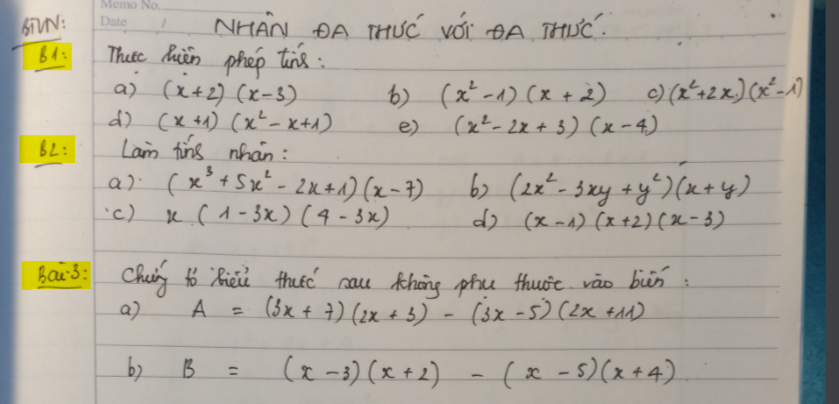
tách ra
Thế bạn lm cho mik câu 3 đc ko ạ ??