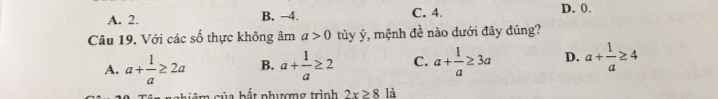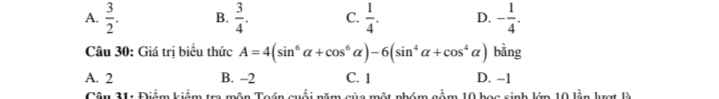K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
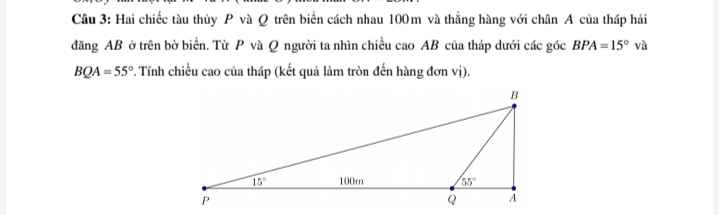
Trong tam giác vuông ABP:
\(tanP=\dfrac{AB}{AP}\Rightarrow AP=\dfrac{AB}{tanP}\Rightarrow PQ+AQ=\dfrac{AB}{tanP}\) (1)
Trong tam giác vuông ABQ:
\(tanQ=\dfrac{AB}{AQ}\Rightarrow AQ=\dfrac{AB}{tanQ}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow PQ+\dfrac{AB}{tanQ}=\dfrac{AB}{tanP}\Rightarrow PQ=AB\left(\dfrac{1}{tanP}-\dfrac{1}{tanQ}\right)\)
\(\Rightarrow AB=\dfrac{PQ}{\dfrac{1}{tanP}-\dfrac{1}{tanQ}}=\dfrac{100}{\dfrac{1}{tan15^0}-\dfrac{1}{tan55^0}}\approx33\left(m\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(A=4\left[\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\right]-6\left[\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a\right]\)
\(=4\left(1-3sin^2a.cos^2a\right)-6\left(1-2sin^2a.cos^2a\right)\)
\(=4-12sin^2a.cos^2a-6+12sin^2a.cos^2a\)
\(=-2\)
30 tháng 6 2023
37:
\(AB=\sqrt{\left(-2-1\right)^2+\left(4-2\right)^2}=\sqrt{13}\)
\(AC=\sqrt{\left(3-1\right)^2+\left(5-2\right)^2}=\sqrt{13}\)
\(BC=\sqrt{\left(3+2\right)^2+\left(5-4\right)^2}=\sqrt{26}\)
Vì AB^2+AC^2=BC^2 và AB=AC
nên ΔABC vuông cân tại A
=>S ABC=1/2*AB*AC=1/2*13=13/2
AH=13/2*2:căn 26=13/căn 26=1/2*căn 26
20 tháng 2 2022
Trường hợp 1: m=0
Bất phương trình sẽ trở thành -3<0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(2m\right)^2-4\cdot m\cdot\left(-3\right)=4m^2+12m\)
Để bất phương trình có nghiệm đúng với mọi x thì \(\left\{{}\begin{matrix}4m\left(m+3\right)< 0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3< m< 0\\m< 0\end{matrix}\right.\Leftrightarrow-3< m< 0\)
Vậy: -3<m<=0
AM
20 tháng 2 2022
Câu 13:
Ta có: \(f\left(x\right)>0\Leftrightarrow3x-m>0\Leftrightarrow3x>m\)
Mà x>1 hay 3x>3
Vậy \(m\le3\)
Đáp án C
AM
20 tháng 2 2022
Câu 14:
(d): x-2y+1=0 hay \(\dfrac{1}{2}x+\dfrac{1}{2}=y\)
Gọi phương trình đường thẳng cần tìm là: y=ax+b
Phương trình cần tìm đi qua A nên ta có: 2=-2a+b
Để phương trình cần tìm vuông góc với (d) thì: \(a.\dfrac{1}{2}=-1\Rightarrow a=-2\)\(\Rightarrow b=-2\)
Vậy phương trình cần tìm là: \(y=-2x-2\)
Đáp án C
