
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36


\(\text{#TNam}\)
`a,`
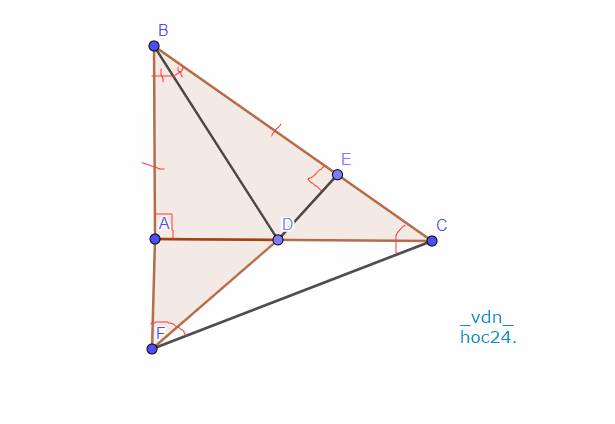
Xét Tam giác `ABD` và Tam giác `EBD` có:
`AB = EB (g``t)`
\(\widehat{ABD}=\widehat{EBD} (\text {tia phân giác}\) \(\widehat{ABE})\)
`\text {BD chung}`
`=> \text {Tam giác ABD = Tam giác EBD (c-g-c)}`
`->`\(\widehat{BAD}=\widehat{BED} (\text {2 góc tương ứng})\)
Mà \(\widehat{BAD}=90^0\)
`->`\(\widehat{BAD}=\widehat{BED}=90^0\)
`->`\(\widehat{BED}\) \(\text {là góc vuông}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BEF` có:
\(\widehat{BAC}=\widehat{BEF}=90^0\)
`BA = BE (g``t)`
\(\widehat{B}\) \(\text {chung}\)
`=> \text {Tam giác BAC = Tam giác BEF (g-c-g)}`
`-> BF = BC (\text {2 cạnh tương ứng})`
Xét Tam giác `BFC:`
`BF = BC (CMT)`
`-> text {Tam giác BFC cân tại B}`
`c,`
Vì Tam giác `BFC` cân tại `B`
`->`\(\widehat{F}=\widehat{C}\)
Xét Tam giác `AFC` và Tam giác `ECF` có:
\(\widehat{F}=\widehat{C}\)
`\text {FC chung}`
\(\widehat{CAF}=\widehat{FEC}=90^0\)
`=> \text {Tam giác AFC = Tam giác ECF (ch-gn)}`

Bài 4:
\(\Leftrightarrow3x-6-1⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)

Câu 4:
a: Xét ΔBAH vuông tại H và ΔBMH vuông tại H có
BH chung
HA=HM
Do đó: ΔBAH=ΔBMH
b: Ta có: ΔBAH=ΔBMH
nên BA=BM
hay ΔBAM cân tại B

4: Ta có: \(x^2+10x+25=0\)
\(\Leftrightarrow x+5=0\)
hay x=-5
5: Ta có: \(x^2-x+\dfrac{1}{4}=0\)
\(\Leftrightarrow x-\dfrac{1}{2}=0\)
hay \(x=\dfrac{1}{2}\)
6: Ta có: \(x^2-10x+25=0\)
nên x-5=0
hay x=5

Câu a nếu bn chứng minh đc a // c r thì bn sẽ lm là:
Vì \(\widehat{IGB}.và.\widehat{GBC}.\text{bù nhau}.\text{nên c//b}\)
a // c; c//b => a // b
\(\text{Xin cái tick}\)
IGB và GBC là 2 góc trong cùng phía bù nhau nhá mk quên