giúp mik câu 1 với ạ chiều mik phải nộp bài 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2M
1
5 tháng 7 2023
a: BC=18-9=9cm
b: C nằm giữa A và B
CA=CB
=>C là trung điểm của AB
c: BK=9/2=4,5cm
=>AK=18-4,5=13,5cm
NH
Ai giúp mik với . Mik cần phải nộp bài vào tối nay . Mik cảm ơn
2
TM
11 tháng 12 2021
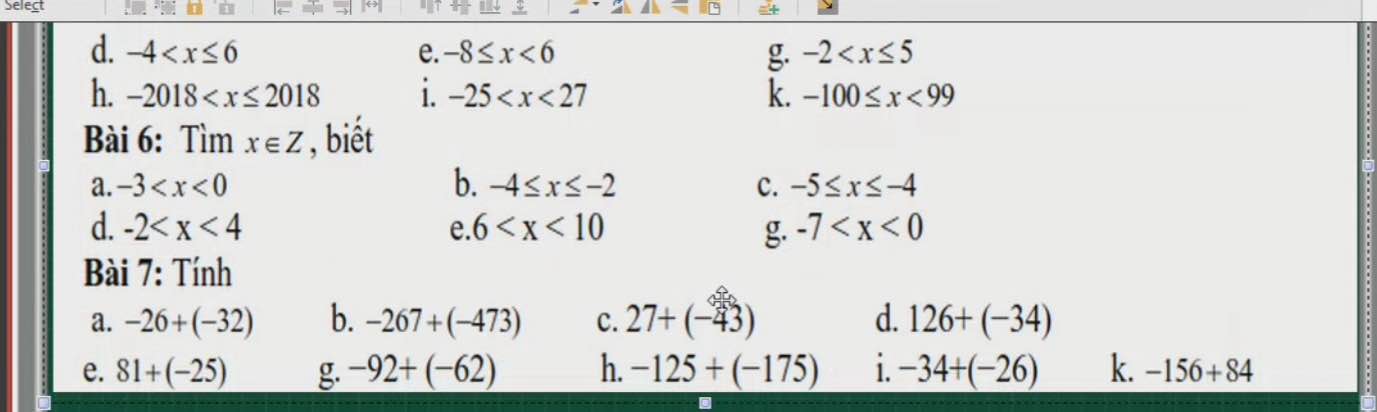
Bài 6:
a/ \(x\in\left\{-2;-1\right\}\)
b/ \(x\in\left\{-4;-3;-2\right\}\)
c/ \(x\in\left\{-5;-4\right\}\)
d/ \(x\in\left\{-1;0;1;2;3\right\}\)
e/ \(x\in\left\{7,8,9\right\}\)
g/ \(x\in\left\{-6;-5;-4;-3;-2;-1\right\}\)
Bài 7:
a/ \(-26+\left(-32\right)=-\left(26+32\right)=-58\)
b/ \(-267+\left(-473\right)=-\left(267+473\right)=-740\)
c/ \(27+\left(-43\right)=-\left(43-27\right)=-16\)
d/ \(126+\left(-34\right)=126-34=92\)
e/ \(81+\left(-25\right)=81-25=56\)
g/ \(-92+\left(-62\right)=-\left(92+62\right)=-154\)
h/ \(-125+\left(-175\right)=-\left(125+175\right)=-300\)
i/ \(-34+\left(-26\right)=-\left(34+26\right)=-60\)
k/ \(-156+84=-\left(156-84\right)=-72\)
QT
2
25 tháng 9 2017
Ta có: 3^2x.3^1+9^x+9^1=120-12=108
=3^2x . 3+9^x+9=108
3^2x . 3+9^x=108-9=99
3^2x . 3+(3^2)^x=99
3^2x .4=99
Cậu kiểm tra lại đề bài được ko
AH
Akai Haruma
Giáo viên
8 tháng 5 2023
Lời giải:
PT $\Leftrightarrow (\frac{x+1}{2022}+1)+(\frac{x+2}{2021}+1)+...+(\frac{x+23}{2000}+1)=0$
$\Leftrightarrow \frac{x+2023}{2022}+\frac{x+2023}{2021}+...+\frac{x+2023}{2000}=0$
$\Leftrightarrow (x+2023)(\frac{1}{2022}+\frac{1}{2021}+...+\frac{1}{2000})=0$
Dễ thấy tổng trong () luôn dương
$\Rightarrow x+2023=0$
$\Leftrightarrow x=-2023$
4 tháng 7 2023
4:
a: OA<OB
=>A nằm giữa O và B
b: A nằm giữa O và B
=>OA+AB=OB
=>AB=4cm
c: OH=HA=OA/2=1,5cm
HB=7-1,5=5,5cm
2:
a: -3/5-x=1/2
=>x=-3/5-1/2=-6/10-5/10=-11/10
b: 3x-5/6=-14/21:2/7=-2/3*7/2=-7/3
=>3x=-7/3+5/6=-14/6+5/6=-9/6=-3/2
=>x=-1/2
c: 1/3(3x-2)+1/4=-9/6=-3/2
=>1/3(3x-2)=-3/2-1/4=-7/4
=>x-2/3=-7/4
=>x=-13/12
Bài 1:
a) Ta có: \( \left|x+2\right|=\left|3-2x\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=2x-3\\x+2=3-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=-3-2\\x+2x=3-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=-5\\3x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{3}\end{matrix}\right.\)
b) Ta có: \(\left|2x-4\right|=\left|3-x\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-4=3-x\\2x-4=x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x+x=3+4\\2x-x=-3+4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=7\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}\\x=1\end{matrix}\right.\)