K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 2 2022
Bài 2:
Đặt AB=a; AC=b; BC=c
AB/AC=3/4
nên a/b=3/4
=>a=3/4b
Theo đề, ta có: \(a^2+b^2=c^2\)
\(\Leftrightarrow b^2\cdot\dfrac{25}{16}=225\)
=>b=12
=>a=9
4 tháng 12 2021
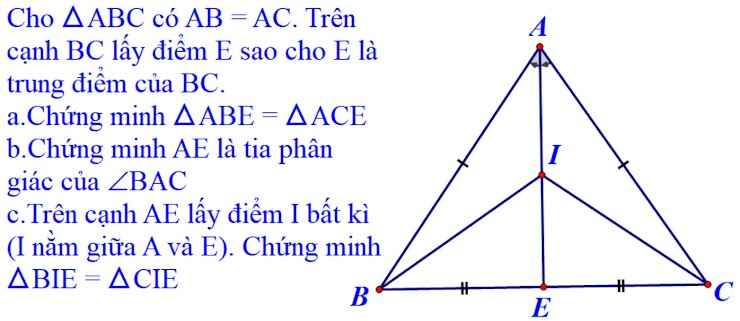
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).
HT
1
24 tháng 10 2020
46.95 + 69.120 / 84.312 - 611
= 212.315 + 212.310.5 / 212.312 - 211.311
= 212. 310.( 35 + 5 ) / 211.311( 2.3 - 1 )
= 2 . 248 / 3 . 5 = 496/15
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a-b}{6-4}=\dfrac{30}{2}=15\)
Do đó: a=90; b=60; c=45