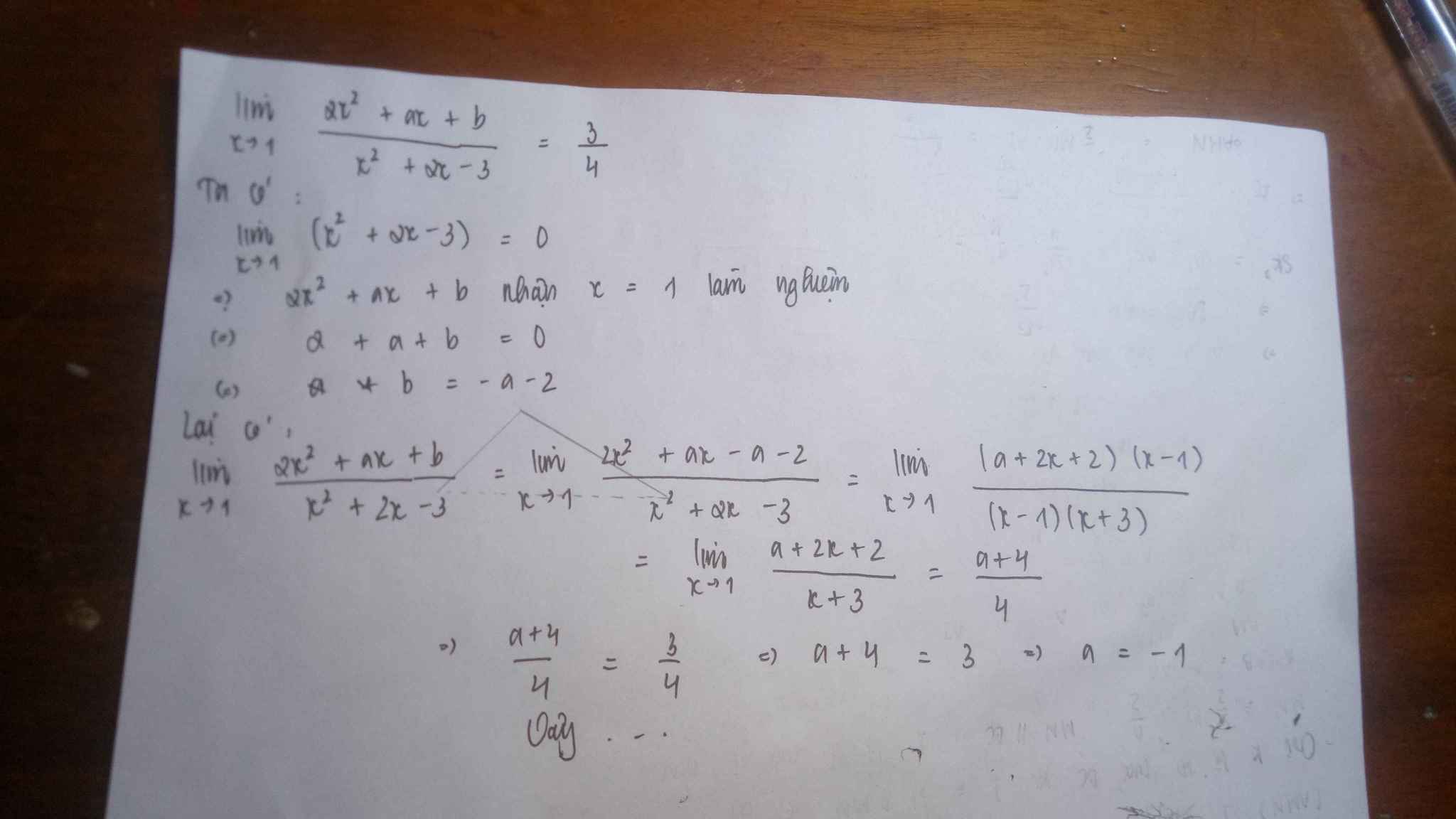Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giới hạn đã cho hữu hạn khi \(2x^2+ax+b=0\) có nghiệm \(x=1\)
\(\Rightarrow2+a+b=0\Rightarrow b=-a-2\)
Ta được: \(\lim\limits_{x\rightarrow1}\dfrac{2x^2+ax-a-2}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{2\left(x-1\right)\left(x+1\right)+a\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2+a\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2x+2+a}{x+1}\)
\(=\dfrac{4+a}{2}=\dfrac{1}{4}\)
\(\Rightarrow a=-\dfrac{7}{2}\Rightarrow b=\dfrac{3}{2}\)

Do \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{x-3}\) hữu hạn \(\Rightarrow f\left(x\right)-2=0\) có nghiệm \(x=3\)
Hay \(f\left(3\right)-2=0\Rightarrow f\left(3\right)=2\)
\(\Rightarrow I=\lim\limits_{x\rightarrow3}\left(\dfrac{f\left(x\right)-2}{x-3}\right).\dfrac{1}{\sqrt{5f\left(x\right)+6}+1}=\dfrac{1}{4}.\dfrac{1}{\sqrt{5.f\left(3\right)+6}+1}\)
\(=\dfrac{1}{4}.\dfrac{1}{\sqrt{5.2+6}+1}=\dfrac{1}{20}\)

Với FX580 hình như tính được luôn
Còn với mọi dòng máy thì:
a. Nhập \(\dfrac{X^2+2X-3}{2X^2-X-1}\) và CALC với \(x=1,000000001\), máy cho kết quả \(\dfrac{4}{3}\)
b. Nhập \(\dfrac{\left|1-3X\right|}{3-X}\) và CALC với \(2,99999999\) (\(x\rightarrow3^-\) nên CALC với giá trị nhỏ hơn 3 1 chút xíu, nếu \(3^+\) thì sẽ CALC với giá trị lớn hơn 3 chút xíu)
Máy cho kết quả rất lớn, dấu dương, hiểu là \(+\infty\)

\(x^2+2x-3=0\) có nghiệm \(x=1\) nên giới hạn đã cho hữu hạn khi \(2x^2+ax+b=0\) cũng có nghiệm \(x=1\)
\(\Rightarrow2.1^2+a.1+b=0\Rightarrow a+b+2=0\Rightarrow b=-a-2\)
Thay vào:
\(\lim\limits_{x\rightarrow1}\dfrac{2x^2+ax-a-2}{x^2+2x-3}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2\right)+a\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2+a\right)}{\left(x-1\right)\left(x+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{2x+2+a}{x+3}=\dfrac{4+a}{4}=\dfrac{3}{4}\)
\(\Rightarrow4+a=3\Rightarrow a=-1\Rightarrow b=-a-2=-1\)

Trình bày công thức các thứ khá dài nên tôi thử nói hướng, nếu bạn hiểu đc và làm đc thì ok còn nếu k hiểu thì bảo mình, mình làm full cho
Bây giờ phân tích mẫu trước, ra (x-1)2(x+2)
Để cái lim này nó ra đc 1 số thực thì tử và mẫu cùng phải triệt tiêu (x-1)2 đi, tức là tử phải chia hết (x-1)2, tức là tử cũng phải có nghiệm kép x=1
Do đó \(\left\{{}\begin{matrix}f\left(1\right)=0\\f'\left(1\right)=0\end{matrix}\right.\)

Tham khảo:
Vì hàm số có giới hạn hữu hạn tại x=1 nên biểu thức tử nhận x=1 làm nghiệm, hay 1+a+b=0.
Áp dụng vào giả thiết, được
\(^{lim}_{x\rightarrow1}\dfrac{x^2+ax-1-a}{x^2-1}=-\dfrac{1}{2}\Leftrightarrow^{lim}_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x+1+a\right)}{\left(x-1\right)\left(x+1\right)}=-\dfrac{1}{2}\)
\(\Leftrightarrow^{lim}_{x\rightarrow1}\dfrac{x+1+a}{x+1}=-\dfrac{1}{2}\Leftrightarrow\dfrac{2+a}{2}=-\dfrac{1}{2}\Leftrightarrow a=-3\)
\(\Rightarrow b=2\)
Lời giải:
Vì $x^2-1\to 0$ khi $x\to 1$ nên để giới hạn đã cho hữu hạn thì $x^2+ax+b$ nhận $x=1$ là nghiệm
$\Leftrightarrow 1+a+b=0$
$\Leftrightarrow b=-a-1$
Khi đó:
\(\lim\limits_{x\to 1}\frac{x^2+ax+b}{x^2-1}=\lim\limits_{x\to 1}\frac{x^2+ax-a-1}{x^2-1}=\lim\limits_{x\to 1}\frac{(x-1)(x+1+a)}{(x-1)(x+1)}=\lim\limits_{x\to 1}\frac{x+a+1}{x+1}\)
\(=\frac{a+2}{2}=\frac{-1}{2}\Rightarrow a+2=-1\Rightarrow a=-3\)
$b=-a-1=3-1=2$

Đề là \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-5}{x-3}\) hay \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-15}{x-3}\) em?
\(\dfrac{f\left(x\right)-5}{x-3}\) thì giới hạn bên dưới ko phải dạng vô định, kết quả là vô cực