
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
c, \(sin\left(\dfrac{\pi}{3}-x\right)=-\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}-x=arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\\dfrac{\pi}{3}-x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\x=-\dfrac{2\pi}{3}+arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
d, \(sin4x=\dfrac{2}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=arcsin\dfrac{2}{3}+k2\pi\\4x=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\end{matrix}\right.\)
1.
e, \(2sin2x+\sqrt{2}=0\)
\(\Leftrightarrow sin2x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x=sin\left(-\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\)

1:
(SAB), (SBC) vuông góc (BAC)
=>SB vuông góc (ABC)
AC vuông góc AB,SB
=>AC vuông góc (SAB)
=>AC vuông góc BH
mà SA vuông góc BH
nên BH vuông góc (SAC)
=>BH vuông góc SC
mà SC vuông góc BK
nên SC vuông góc (BHK)
c: (SH;(BHK))=góc SHK=(SA;BHK)
BC=BA/cos60=2a
SC=căn SB^2+BC^2=ăcn 5
SB^2=SK*SC
=>SK=a*căn 5/5
SA=căn SB^2+AB^2=a*căn 2
SB^2=SH*SA
=>SH=a*căn 2/2
sin SHK=căn 10/5
=>góc SHK=39 độ



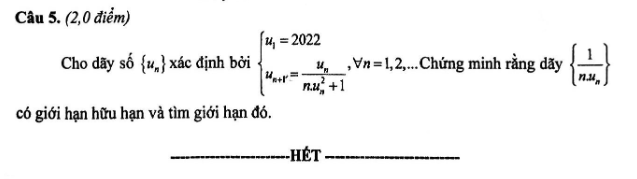
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)

Tất cả \(k\in Z\)
1.
a. \(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
Đáp án trong đề bị sai
b.
\(\Leftrightarrow\dfrac{1}{2}cos7x-\dfrac{\sqrt{3}}{2}sin7x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(7x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}7x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\\7x+\dfrac{\pi}{3}=-\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}7x=\dfrac{5\pi}{12}+k2\pi\\7x=-\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\\x=-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\end{matrix}\right.\)
Do \(\dfrac{2\pi}{5}\le x\le\dfrac{6\pi}{7}\Rightarrow\left[{}\begin{matrix}\dfrac{2\pi}{5}\le\dfrac{5\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\\\dfrac{2\pi}{5}\le-\dfrac{13\pi}{84}+\dfrac{k2\pi}{7}\le\dfrac{6\pi}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{143}{120}\le k\le\dfrac{67}{24}\\\dfrac{233}{120}\le k\le\dfrac{85}{24}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=1\\k=\left\{2;3\right\}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{53\pi}{84};\dfrac{5\pi}{12};\dfrac{59\pi}{84}\right\}\)

Kẻ \(HE\perp AD\) , do tam giác ABD đều \(\Rightarrow HE=\dfrac{a\sqrt{3}}{2}\) ; \(AE=\dfrac{1}{4}AD\)
\(\Rightarrow AE=BM\Rightarrow\) tứ giác AEBM là hình bình hành \(\Rightarrow\) H đồng thời là trung điểm ME
Kẻ \(HK\perp SE\Rightarrow HK\perp\left(SAD\right)\)
a. Ta có: \(SH=HE\Rightarrow\) tam giác SHE vuông cân tại H
\(\Rightarrow\) K đồng thời là trung điểm SE
\(\Rightarrow\) KH là đường trung bình tam giác SME \(\Rightarrow SM||HK\)
\(\Rightarrow SM\perp\left(SAD\right)\)
b. Từ C kẻ \(CX\perp\left(SAD\right)\Rightarrow\widehat{CSX}\) là góc giữa SC và (SAD) đồng thời \(CX=d\left(C;\left(SAD\right)\right)\)
\(\Rightarrow sin\alpha=sin\widehat{CSX}=\dfrac{CX}{SC}\)
Từ M kẻ \(MI\perp SE\Rightarrow MI||HK\Rightarrow MI\perp\left(SAD\right)\)
\(\Rightarrow MI=d\left(M;\left(SAD\right)\right)\)
Mà \(CM||AD\Rightarrow CM||\left(SAD\right)\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(M;\left(SAD\right)\right)\)
\(\Rightarrow CX=MI\)
HK là đường trung bình tam giác MIE \(\Rightarrow MI=2HK\)
\(MI=2HK=\dfrac{2SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+\dfrac{3a^2}{4}}}\)
\(SC=\sqrt{SH^2+CH^2}=\sqrt{SH^2+MH^2+CM^2}=\sqrt{SH^2+HE^2+CM^2}\)
\(=\sqrt{SH^2+7a^2}\)
\(\Rightarrow sin\alpha=\dfrac{SH.a\sqrt{3}}{\sqrt{SH^2+7a^2}.\sqrt{SH^2+\dfrac{3a^2}{4}}}=\dfrac{a\sqrt{3}}{\sqrt{SH^2+\dfrac{21a^4}{4SH^2}+\dfrac{31}{4}a^2}}\le\dfrac{a\sqrt{3}}{\sqrt{2\sqrt{\dfrac{21a^4}{4}}+\dfrac{31}{4}a^2}}\)
Dấu "=" xảy ra khi \(SH^2=\dfrac{21a^4}{4SH^2}\Rightarrow SH=a\sqrt[4]{\dfrac{21}{4}}\)
Em kiểm tra lại tính toán

Khá dễ dàng nhận ra do tính chất đường trung bình nên tam giác \(A_1B_1C_1\) chia tam giác ABC thành 4 tam giác có diện tích bằng nhau
\(\Rightarrow S_{A_1B_1C_1}=\dfrac{1}{4}S_{ABC}\)
Do đó \(S_1;S_2...;S_{50}\) lập thành 1 cấp số nhân với \(u_1=S_1=\dfrac{6}{4}=\dfrac{3}{2}\) và \(q=\dfrac{1}{4}\)
\(\Rightarrow S\left(50\right)=\dfrac{3}{2}.\dfrac{1-\left(\dfrac{1}{4}\right)^{50}}{1-\dfrac{1}{4}}\)
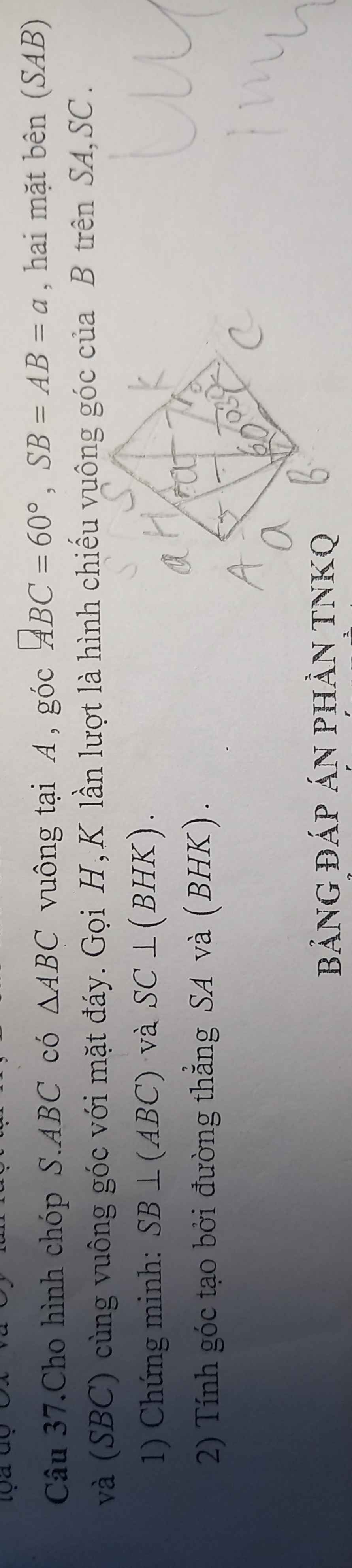
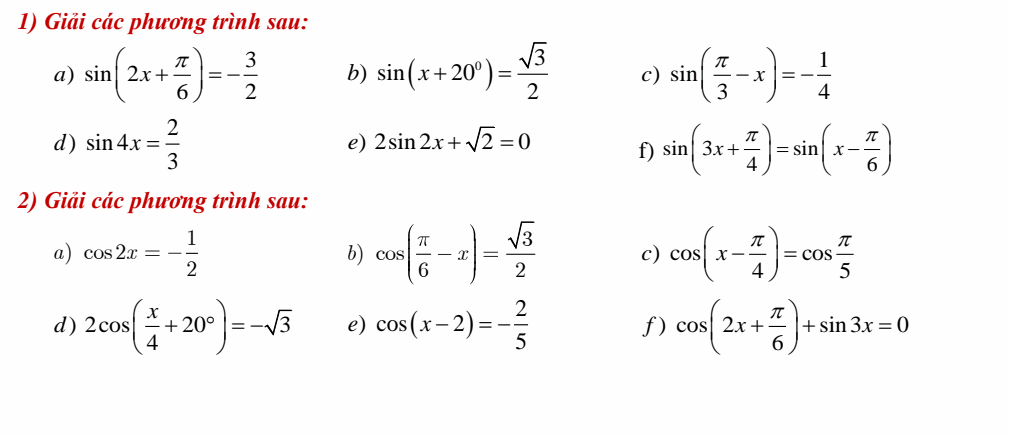








 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ
 giúp em với em cảm ơn nhiều lắmmm ạ
giúp em với em cảm ơn nhiều lắmmm ạ

1:
(SAB), (SBC) vuông góc (BAC)
=>SB vuông góc (ABC)
AC vuông góc AB,SB
=>AC vuông góc (SAB)
=>AC vuông góc BH
mà SA vuông góc BH
nên BH vuông góc (SAC)
=>BH vuông góc SC
mà SC vuông góc BK
nên SC vuông góc (BHK)
c: (SH;(BHK))=góc SHK=(SA;BHK)
BC=BA/cos60=2a
SC=căn SB^2+BC^2=ăcn 5
SB^2=SK*SC
=>SK=a*căn 5/5
SA=căn SB^2+AB^2=a*căn 2
SB^2=SH*SA
=>SH=a*căn 2/2
sin SHK=căn 10/5
=>góc SHK=39 độ