K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 8 2021
Để M nguyên thì \(5⋮\sqrt{a}+1\)
\(\Leftrightarrow\sqrt{a}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow\sqrt{a}\in\left\{0;4\right\}\)
hay \(a\in\left\{0;16\right\}\)
24 tháng 8 2021
Tham khảo: Cho tứ giác ABCD có góc C + góc D = 90 độ. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng nằm trên 1 đường tròn - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
24 tháng 8 2021
Xét ΔABD có
M là trung điểm của AB
S là trung điểm của AD
Do đó: MS là đường trung bình của ΔBAD
Suy ra: MS//BD và \(MS=\dfrac{BD}{2}\left(1\right)\)
mà BD\(\perp\)AC
nên MS\(\perp\)AC
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
và AC\(\perp\)MS
nên MN\(\perp\)MS
Xét ΔBCD có
N là trung điểm của BC
R là trung điểm của CD
Do đó: RN là đường trung bình của ΔBCD
Suy ra: RN//BD và \(RN=\dfrac{BD}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra MS//NR và MS=NR
Xét tứ giác MSRN có
MS//NR
MS=NR
Do đó: MSRN là hình bình hành
mà \(\widehat{SMN}=90^0\)
nên MSRN là hình chữ nhật
Suy ra: M,S,R,N cùng thuộc 1 đường tròn
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 8 2021
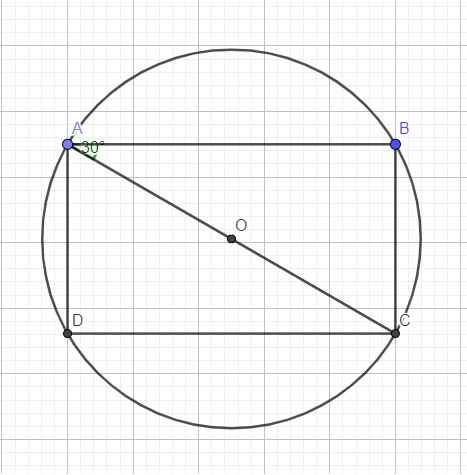
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{ABC}=90^0\Rightarrow\) B là góc nội tiếp chắn nửa đường tròn hay AC là đường kính
\(\Rightarrow AC=2R=100\left(cm\right)\)
Trong tam giác vuông ABC ta có:
\(sin\widehat{BAC}=\dfrac{BC}{AC}\Rightarrow BC=AC.sin\widehat{BAC}=100.sin30^0=50\left(cm\right)\)
\(\Rightarrow AD=BC=50\left(cm\right)\)
Áp dụng định lý Pitago:
\(AB=\sqrt{AC^2-BC^2}=50\sqrt{3}\left(cm\right)=CD\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
a.
\(\Delta=\left(-5\right)^2-4.3.2=25-24=1>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\\x_1x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(4A=x_1^2+x_2^2-x_1x_2=\left(x_1^2+x_2^2+2x_1x_2\right)-3x_1x_2\)
\(4A=\left(x_1+x_2\right)^2-3x_1x_2\)
\(4A=\left(\dfrac{5}{3}\right)^2-3.\left(\dfrac{2}{3}\right)=\dfrac{7}{9}\)
\(\Rightarrow A=\dfrac{7}{36}\)
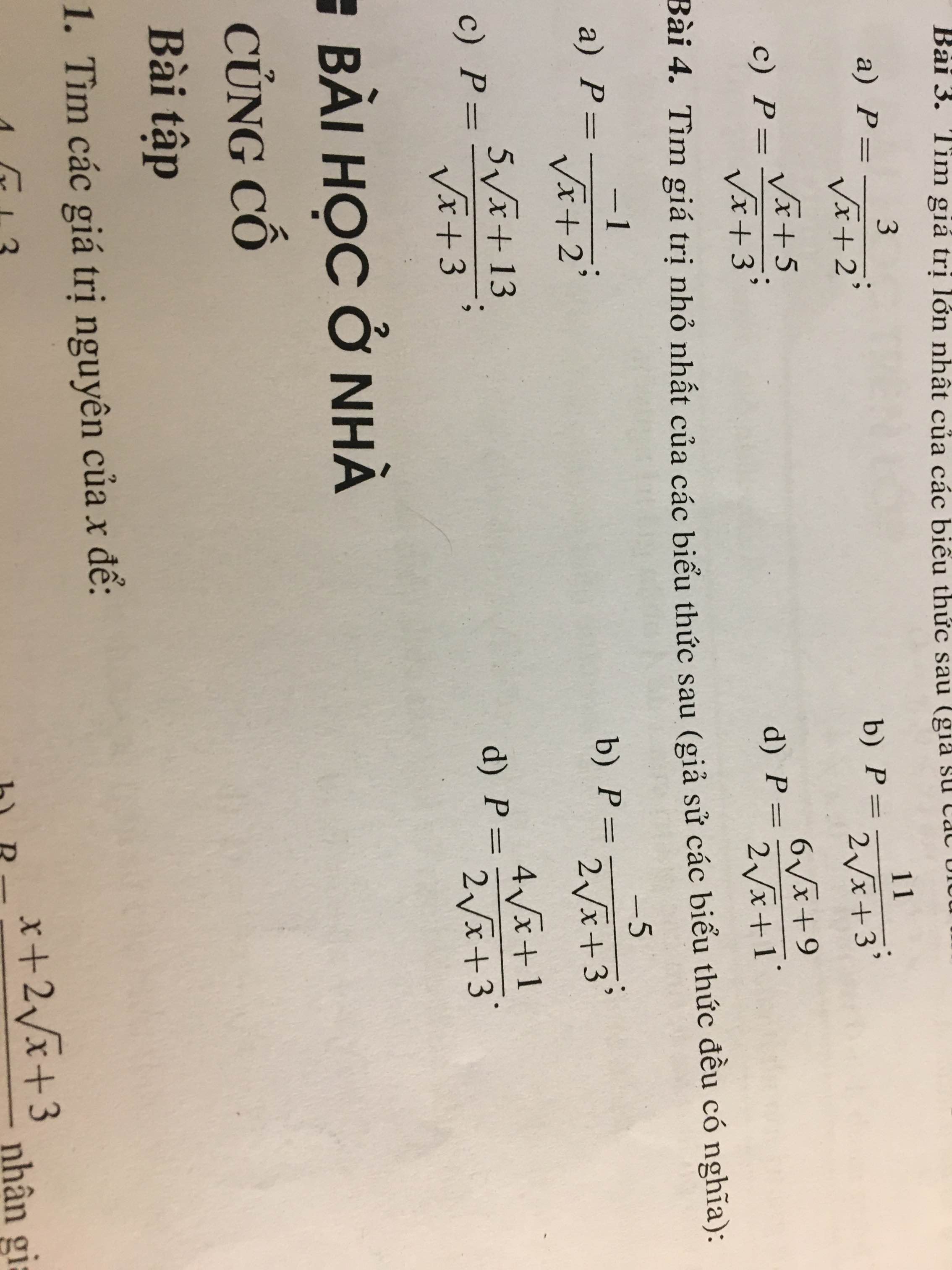
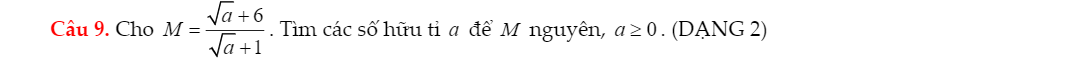
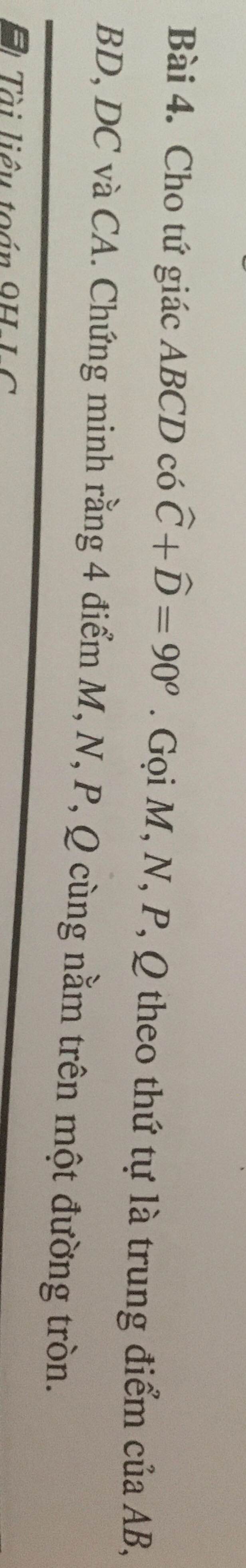
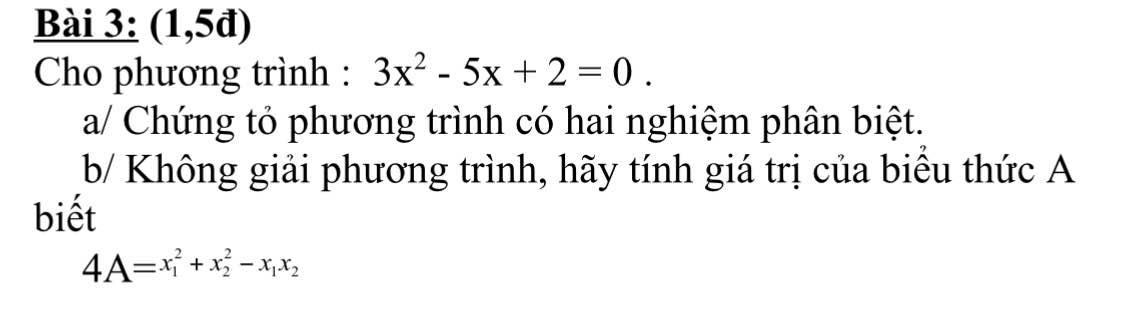
4d.
\(P=\dfrac{4\sqrt{x}+1}{2\sqrt{x}+3}\)
\(=\dfrac{2\left(2\sqrt{x}+3\right)}{2\sqrt{x}+3}-\dfrac{5}{2\sqrt{x}+3}\)
\(=2-\dfrac{5}{2\sqrt{x}+3}\)
\(\ge2-\dfrac{5}{2.0+3}=\dfrac{1}{3}\)
\(\Rightarrow minP=\dfrac{1}{3}\Leftrightarrow x=0\)