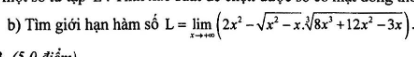Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ

\(L=\lim\limits_{x\rightarrow+\infty}\left(2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\right)\)
Đặt \(f\left(x\right)=2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\)
Ta có:
\(2.f\left(x\right)=4x^2-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(4x^2-1\right)-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)+\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
Đặt \(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(=\dfrac{\left(2x-1\right)\left(8x^3+12x^2+6x+1-8x^3-12x^2+3x\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(=\dfrac{\left(2x-1\right)\left(9x+1\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}A\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2-\dfrac{1}{x}\right)\left(9+\dfrac{1}{x}\right)}{\left(2+\dfrac{1}{x}\right)^2+\sqrt[3]{\left(8+\dfrac{12}{x}-\dfrac{3}{x^2}\right)^2}+\left(2+\dfrac{1}{x}\right)\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}\)
\(=\dfrac{2.9}{2^2+4+2.2}\)
\(=\dfrac{3}{2}\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(=\dfrac{\left(4x^2-4x+1-4x^2+4x\right).\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(=\dfrac{\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}B\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}{2-\dfrac{1}{x}+\sqrt{4-\dfrac{4}{x}}}\)
\(=\dfrac{2}{2+2}\)
\(=\dfrac{1}{2}\)
\(\Rightarrow2L=\lim\limits_{x\rightarrow+\infty}\left[2f\left(x\right)\right]\)
\(=\lim\limits_{x\rightarrow+\infty}\left[1+A\left(x\right)+B\left(x\right)\right]\)
\(=1+\lim\limits_{x\rightarrow+\infty}A\left(x\right)+\lim\limits_{x\rightarrow+\infty}B\left(x\right)\)
\(=1+\dfrac{3}{2}+\dfrac{1}{2}\)
\(=3\)
\(\Rightarrow L=\dfrac{3}{2}\)

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.


Đặt \(f\left(x\right)=x^2sinx+x.cosx+1\)
Hàm \(f\left(x\right)\) liên tục trên mọi khoảng thuộc R
Ta có: \(f\left(0\right)=1>0\)
\(f\left(\pi\right)=-\pi+1< 0\)
\(\Rightarrow f\left(0\right).f\left(\pi\right)< 0\Rightarrow\) phương trình \(f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\pi\right)\)
Hay pt đã cho luôn có nghiệm trên R

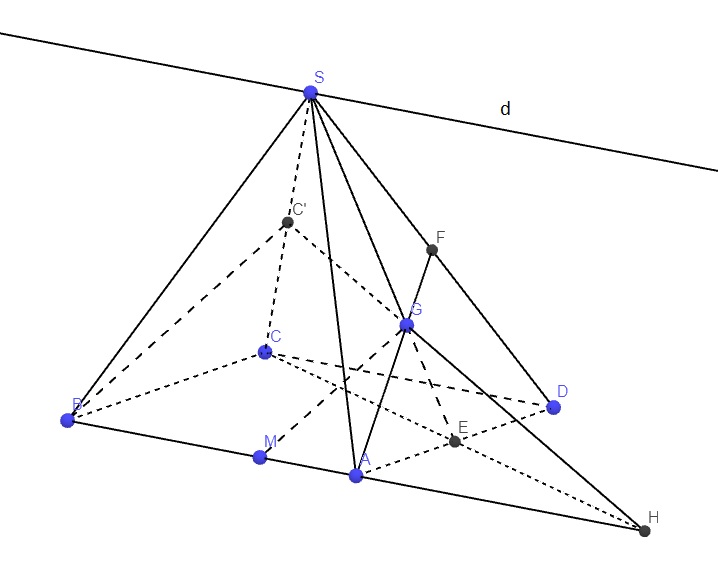
a.
Qua S kẻ đường thẳng d song song AB
Do \(\left\{{}\begin{matrix}AB\in\left(SAB\right)\\CD\in\left(SCD\right)\\AB||CD\\S\in\left(SAB\right)\cap\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
Gọi E là trung điểm AD, kéo dài AG cắt SD tại F \(\Rightarrow F\) là trung điểm SD (do G là trọng tâm SAD)
AM thuộc AB nên AM cắt SB tại B \(\Rightarrow B'\) trùng B
Trong mp (SCD), qua F kẻ đường thẳng song song CD cắt SC tại C'
\(\Rightarrow C'\) là trung điểm SC (do F là trung điểm SD)
Trong mp (ABCD), kéo dài AB và CE cắt nhau tại H
3 mp (SCE), (ABCD), (AGM) cắt nhau theo 3 giao tuyến phân biệt AB, CE, C'G, mà AB và CE cắt nhau tại H \(\Rightarrow\) 3 đường thẳng đồng quy tại H (theo t/c giao tuyến 3 mp cắt nhau)
Hay C',G,H thẳng hàng
\(AE||CB\) ; \(AE=\dfrac{1}{2}AD=\dfrac{1}{2}CB\Rightarrow\) AE là đường trung bình tam giác HCB
\(\Rightarrow A\) là trung điểm BH và E là trung điểm CH
\(\Rightarrow G\) là trọng tâm tam giác SCH
\(\Rightarrow\dfrac{HG}{HC'}=\dfrac{2}{3}\) (1)
Theo giả thiết \(MB=2MA\Rightarrow AB-MA=2MA\Rightarrow MA=\dfrac{1}{3}AB=\dfrac{1}{3}AH\)
\(\Rightarrow\dfrac{HM}{BH}=\dfrac{AH+AM}{2AH}=\dfrac{AH+\dfrac{1}{3}AH}{2AH}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{HG}{HC'}=\dfrac{HM}{BH}\Rightarrow MG||BC'\)
Hay \(MG||B'C'\) (do B trùng B')
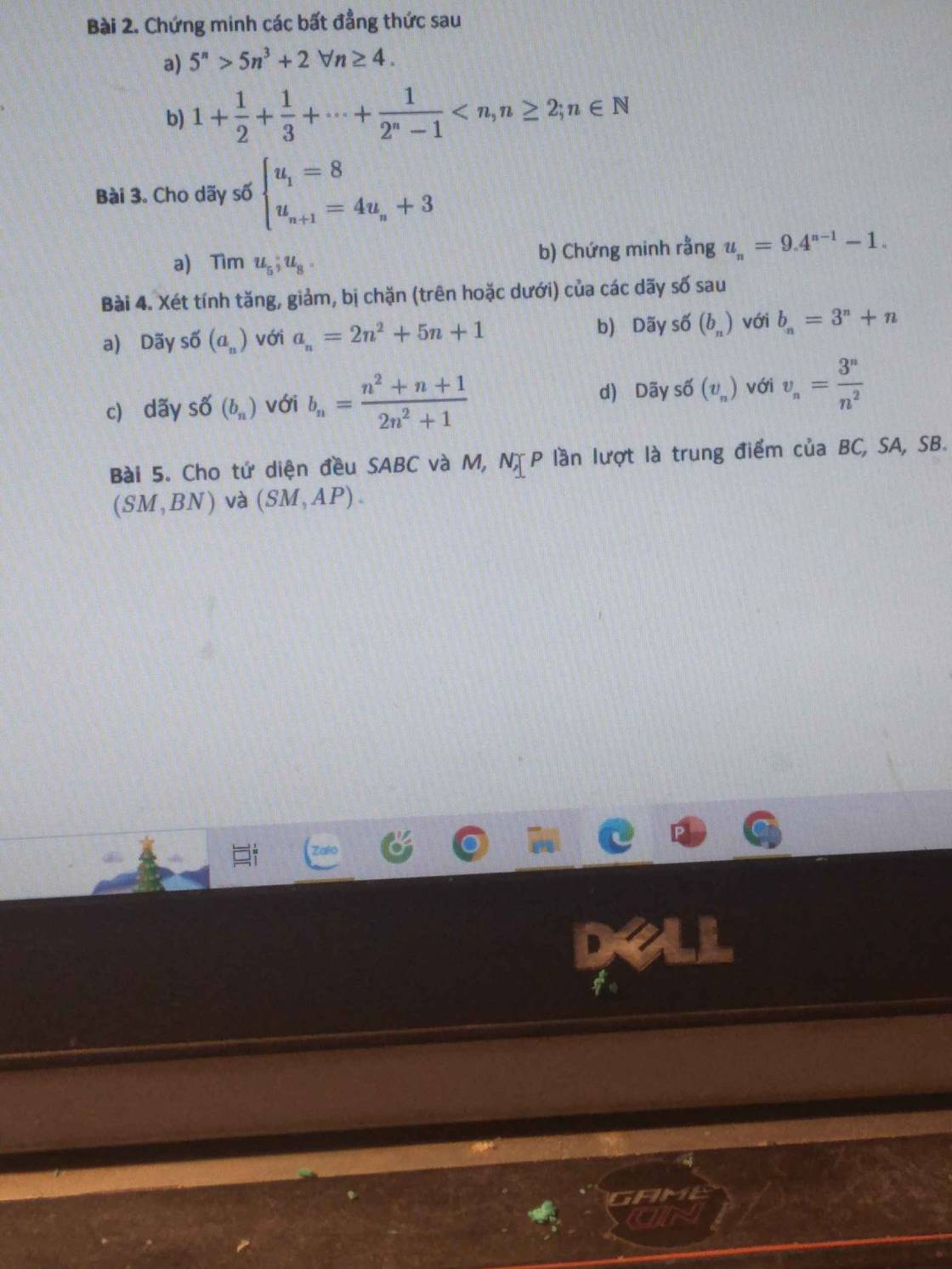 giúp em bài 4 với ạ. Pls
giúp em bài 4 với ạ. Pls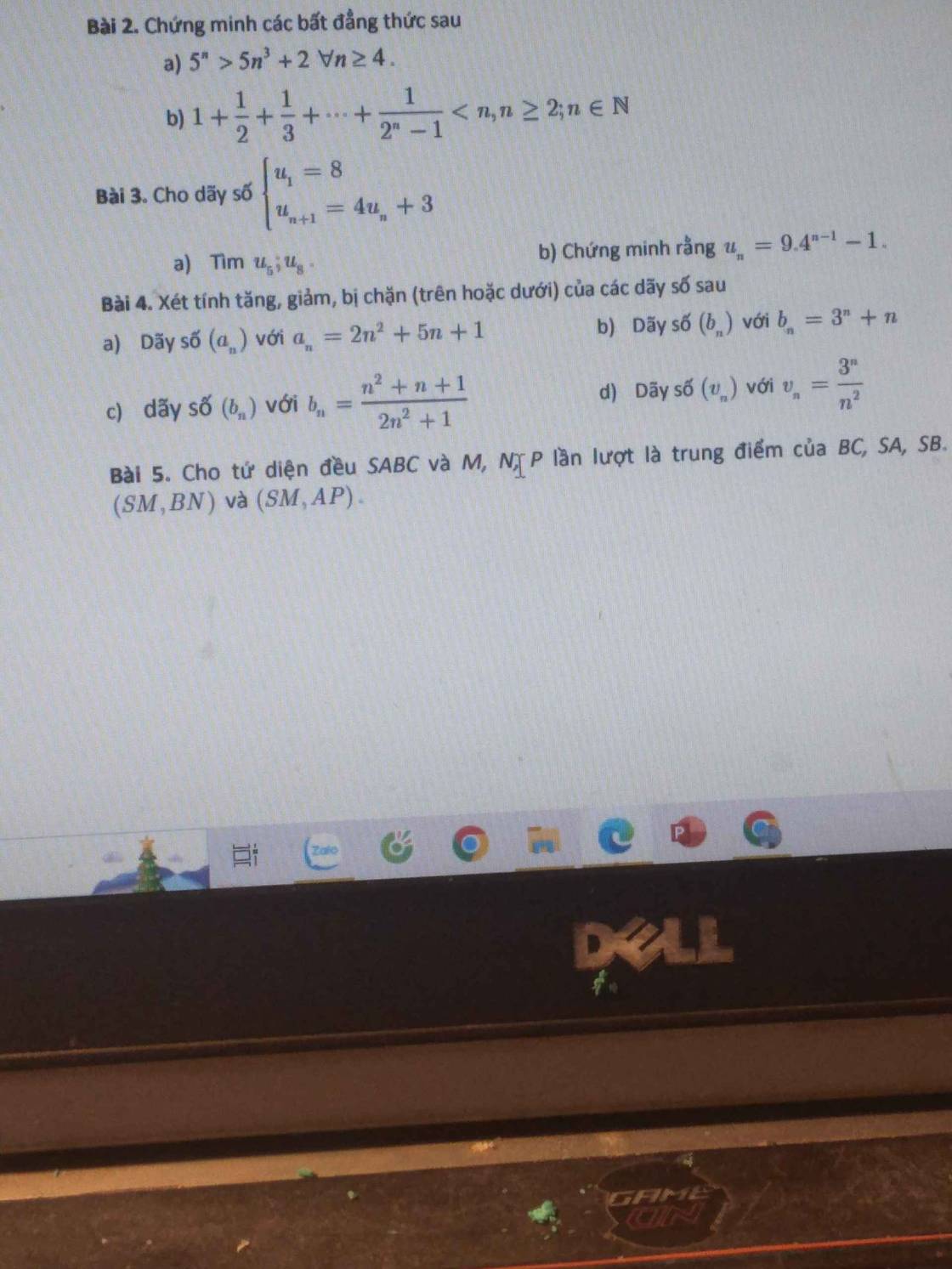 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ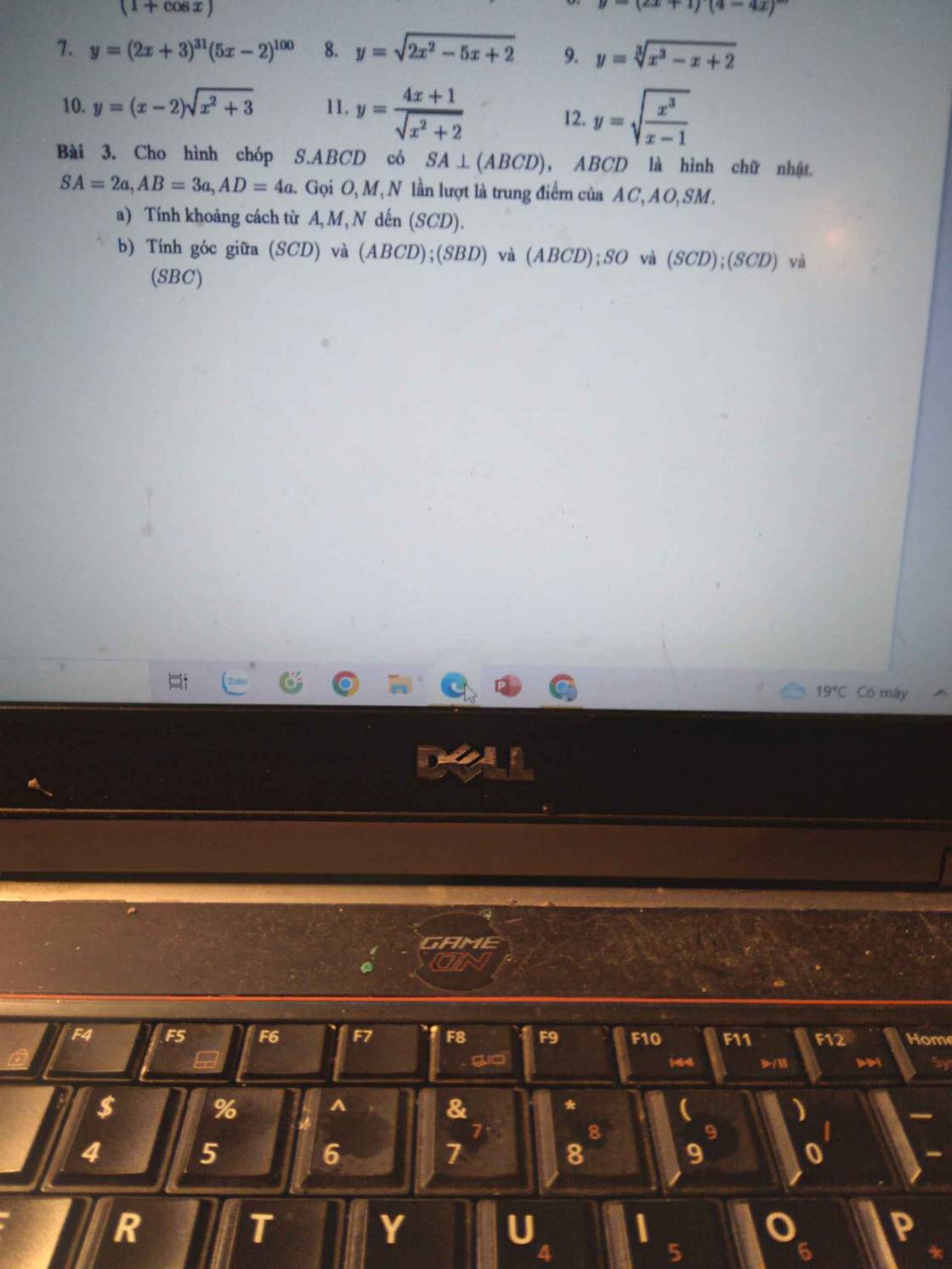 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ