K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 10 2021
Bài 1:
a: \(A=\sqrt{18}-2\sqrt{50}+3\sqrt{8}\)
\(=3\sqrt{2}-10\sqrt{2}+6\sqrt{2}\)
\(=-\sqrt{2}\)
HN
7 tháng 10 2021
Bài 1:
c) \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{8-2\sqrt{7}} + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{(\sqrt{7})^2 - 2\sqrt{7}+1} + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{(\sqrt{7}-1)^2} + \sqrt{2} \)do
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - |\sqrt{7}-1| + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{7}+1 + \sqrt{2} \) (do \(\sqrt{7} > 1 \))
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - (\sqrt{7} - \sqrt{2}) +1 \)
⇔ \(C=\dfrac{5-(\sqrt{7} - \sqrt{2})(\sqrt{7}+\sqrt{2})}{\sqrt{7}+\sqrt{2}} +1 \)
⇔ \(C=\dfrac{5-7+2}{\sqrt{7}+\sqrt{2}} +1 =\dfrac{0}{\sqrt{7}+\sqrt{2}} +1 \)
⇔ \(C = 0 + 1 = 1\)
Vậy \(C=1\)
HN
7 tháng 10 2021
Bài 3:
c) Ta có: \(M=\dfrac{Q}{P} \)
⇔ \(M=\dfrac{\dfrac{\sqrt{x}}{\sqrt{x}-2}}{\dfrac{\sqrt{x}+5}{\sqrt{x}-2} } \)
⇔ \(M=\dfrac{\sqrt{x}}{\sqrt{x}+5} \)
Mà: \(M<\dfrac{1}{2} \) ⇔ \(\dfrac{\sqrt{x}}{\sqrt{x}+5} <\dfrac{1}{2} \)
⇒ \(2\sqrt{x} < \sqrt{x}+5 \) (nhân 2 vế với \(2.(\sqrt{x} +5) >0\))
⇔ \(\sqrt{x}<5 \) ⇔ \(x<25\)
Kết hợp điều kiện ban đầu, ta đc:
Vậy khi \(0≤x<25\) và \(x≠4\) thì \(M=\dfrac{Q}{P} < \dfrac{1}{2} \)
8 tháng 9 2021
\(\left(\sqrt{7}-2\right)^2=11-4\sqrt{7}\)
\(\left(3-\sqrt{7}\right)^2=16-6\sqrt{7}=11-4\sqrt{7}+5-2\sqrt{7}\)
mà \(5-2\sqrt{7}< 0\)
nên \(\sqrt{7}-2< 3-\sqrt{7}\)
29 tháng 8 2021
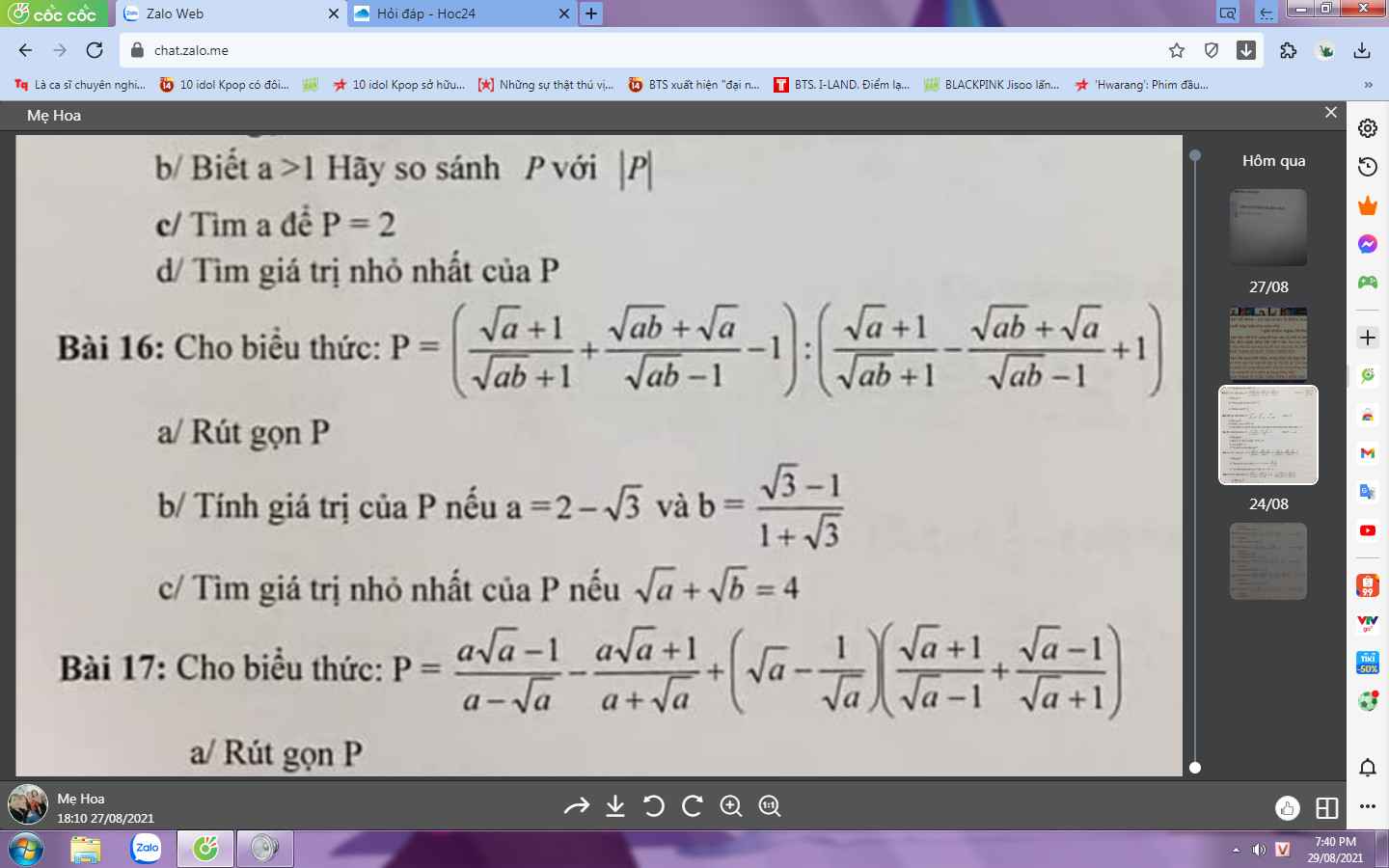
Bài 16:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)
