K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 10 2021
3: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB=12.5\left(cm\right)\)
\(\Leftrightarrow AC=12.5\sqrt{3}\left(cm\right)\)
AN
2
2 tháng 3 2023
Bài 3.
a. Ta có: \(CK=BK\left(gt\right)\Rightarrow OK\perp BC\)
Ta có: \(\widehat{OIC}=90^o\)
\(\widehat{OKC}=90^o\)
\(\Rightarrow\widehat{OIC}+\widehat{OKC}=90^o+90^o=180^o\)
`=>` Tứ giác CIOK nội tiếp đường tròn
b. Xét \(\Delta AID\) và \(\Delta CIB\), có:
\(\widehat{AID}=\widehat{CIB}=90^o\left(gt\right)\)
\(\widehat{ADI}=\widehat{CBI}\) ( cùng chắn \(\stackrel\frown{AC}\) )
Vậy \(\Delta AID\sim\Delta CIB\) ( g.g)
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{ID}{IB}\)
\(\Leftrightarrow IC.ID=IA.IB\)
c. Kẻ \(DM\perp AC\)
Ta có: \(\widehat{ACB}=90^o\) ( góc nt chắn nửa đtròn )
`->` Tứ giác DMCK là hình chữ nhật
\(\rightarrow DK\perp BC\)
Mà \(OK\perp BC\)
\(\Rightarrow\) 3 điểm D,O,K thẳng hàng
1 tháng 9 2021
1B:
a: Ta có: \(N=\sqrt{8}+\sqrt{32}+\sqrt{108}-\sqrt{27}\)
\(=2\sqrt{2}+4\sqrt{2}+6\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{2}+3\sqrt{3}\)
b: Ta có: \(M=\dfrac{2}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}\)
\(=4-2\sqrt{3}-2-\sqrt{3}\)
\(=2-3\sqrt{3}\)
NT
1
24 tháng 7 2021
3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
9 tháng 9 2021
a: Ta có: \(A=\sin^21^0+\sin^22^0+...+\sin^288^0+\sin^289^0\)
\(=\left(\sin^21^0+\sin^289^0\right)+...+\sin^245^0\)
\(=1+1+...+1+\dfrac{1}{2}\)
\(=\dfrac{89}{2}\)
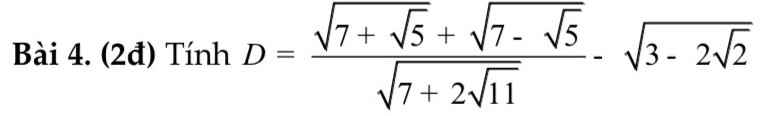
Bài 4:
a: Ta có: \(IA=IB=\dfrac{AB}{2}\)
\(DK=KC=\dfrac{DC}{2}\)
mà AB=DC
nên IA=IB=DK=KC
Xét tứ giác IBKD có
IB//DK
IB=DK
Do đó: IBKD là hình bình hành
b: Xét tứ giác AIKD có
AI//DK
AI=DK
Do đó: AIKD là hình bình hành
Suy ra: Hai đường chéo AK và DI cắt nhau tại trung điểm của mỗi đường
mà AK cắt DI tại E
nên E là trung điểm của DI
Suy ra: \(EI=\dfrac{DI}{2}\left(1\right)\)
Xét tứ giác BIKC có
BI//KC
BI=KC
Do đó: BIKC là hình bình hành
Suy ra: Hai đường chéo IC và BK cắt nhau tại trung điểm của mỗi đường
mà IC cắt BK tại F
nên F là trung điểm của BK
\(\Leftrightarrow KF=\dfrac{BK}{2}\left(2\right)\)
Ta có: IBKD là hình bình hành
nên \(ID=BK\left(3\right)\) và ID=BK
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra EI//KF và EI=KF
Xét tứ giác IEKF có
IE//KF
IE=KF
Do đó: IEKF là hình bình hành
Bài 4:
c: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
Suy ra: Hai đường chéo AC và IK cắt nhau tại trung điểm của mỗi đường\(\left(4\right)\)
Ta có: EIFK là hình bình hành
nên hai đường chéo EF và IK cắt nhau tại trung điểm của mỗi đường\(\left(5\right)\)
Từ \(\left(4\right),\left(5\right)\) suy ra AC,EF,IK đồng quy