
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a) `
`P`(`x`)`=3x^3 -5x^2 -x^3 -6x+2`
`=2x^3 -5x^2 -6x+2`
`Q`(`x`)`=-2x^3 -7x +1 +2x^2 -x`
`=-2x^3 +2x^2 -8x+1`
`b)`
P(x) `+ `Q(x)`=(2x^3 -5x^2 -6x+2)+(-2x^3 +2x^2 -8x+1)`
`=2x^3 -5x^2 -6x+2-2x^3 +2x^2 -8x+1`
`=-3x^2 -14x+3`
P(x) `- `Q(x)`=(2x^3 -5x^2 -6x+2)-(-2x^3 +2x^2 -8x+1)`
`=2x^3 -5x^2 -6x+2+2x^3 -2x^2 +8x-1`
`=4x^3 -7x^2 +2x +1`

Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
d: \(AH^2-AN^2=HN^2\)
\(BH^2-BM^2=MH^2\)
mà HN=MH
nên \(AH^2-AN^2=BH^2-BM^2\)
hay \(AH^2+BM^2=BH^2+AN^2\)

TL:
10. A(1;-2) (hoặc bn có thể chọn điểm khác vs tạo độ khác cx đc)
11. y tỉ lệ thuận với x

a, Vì AC⊥AB và BD⊥AB nên AC//BD
b, Vì AC//BD nên \(\widehat{D_1}=\widehat{ACD}\) (so le trong)
Mà \(\widehat{ACD}+\widehat{C_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{ACD}=\widehat{D_1}=180^0-70^0=110^0\)

Ta có \(MN\perp AC\Rightarrow\) Tam giác AHC vuông tại H ; Tam giác AHB vuông tại H
Do \(\widehat{A_1}=\widehat{A_2}\) , \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)
Suy ra được 2 góc còn lại của 2 tam giác bằng nhau
\(a,\) Xét \(\Delta AHC\) và \(\Delta AHB:\)
Có 3 góc trong tam giác đều bằng nhau \(\Rightarrow\Delta AHC=\Delta AHB\left(g-g-g\right)\)
\(b,\) \(\widehat{A_1}=\widehat{A_2}\Rightarrow\) A là đường phân giác của tam giác ABC\(\Rightarrow HC=HB\)
Xét \(\Delta HNC\) và \(\Delta HMB:\)
Có 2 góc bằng nhau \(\widehat{M}=\widehat{N}\left(=90^o\right);\widehat{C}=\widehat{B}\left(cmt\right)\)
Và \(HC=HB\left(cmt\right)\)
\(\Rightarrow\Delta HNC=\Delta HMB\left(g-c-g\right)\)

b: Gọi chiều dài và chiều rộng lần lượt là x,y
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{x+y}{7+5}=\dfrac{48}{12}=4\)
Do đó: x=28; y=20
Diện tích là:
28x20=560(m2)



 dag cần gấp ạ! e c.ơn
dag cần gấp ạ! e c.ơn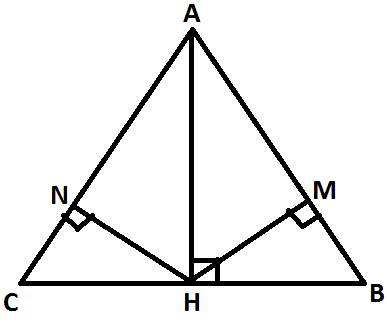
 giúp em với :3 cảm ơn ạaaa <33
giúp em với :3 cảm ơn ạaaa <33
a) a//b vì c cắt a và b vông góc tại điểm A và B
Vì C1 và C2 là hai cặp góc đối đỉnh
⇒ C1=C2 (45o)