K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
Hàm \(f\left(x\right)\) ko xác định khi \(x+4=0\Rightarrow x=-4\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=-4\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
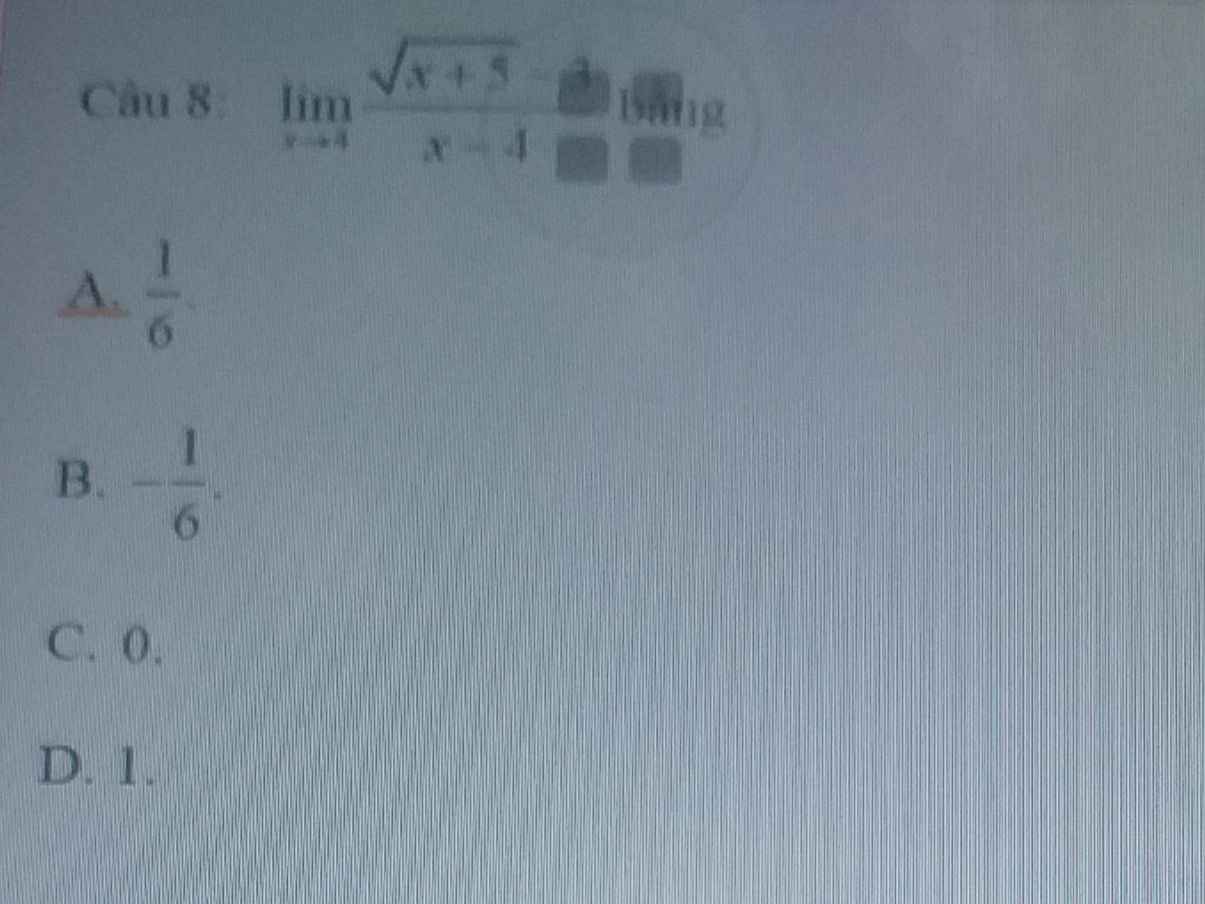
\(\lim\limits_{x\rightarrow4}\dfrac{\sqrt{x+5}-3}{x-4}=\lim\limits_{x\rightarrow4}\dfrac{\left(\sqrt{x+5}-3\right)\left(\sqrt{x+5}+3\right)}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}\)
\(=\lim\limits_{x\rightarrow4}\dfrac{x-4}{\left(x-4\right)\left(\sqrt{x+5}+3\right)}=\lim\limits_{x\rightarrow4}\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{3+3}=\dfrac{1}{6}\)
KB
4 tháng 5 2022
\(y=\dfrac{x-1}{x+2}\left(x\ne-2\right)\Rightarrow y'=\dfrac{\left(x+2\right)-\left(x-1\right)}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)
Giả sử d là tiếp tuyến cần tìm của đths trên
a. d đi qua \(N\left(-1;-2\right)\) . Suy ra : HSG của d : \(\dfrac{3}{\left(-1+2\right)^2}=3\)
PTTT d : \(y=3\left(x+1\right)-2=3x+1\)
b.d có hđtđ \(x_o=3\) \(\Rightarrow y_o=\dfrac{3-1}{3+2}=\dfrac{2}{5};y'=\dfrac{3}{25}\)
PTTT d : \(y=\dfrac{3}{25}\left(x-3\right)+\dfrac{2}{5}=\dfrac{3x}{25}+\dfrac{1}{25}\)
c. Tung độ tiếp điểm yo = 9 nên : \(\dfrac{x_o-1}{x_o+2}=9\Leftrightarrow x_o=-\dfrac{19}{8}\)
y' = 64/3
PTTT d : \(y=\dfrac{64}{3}\left(x+\dfrac{19}{8}\right)+9=\dfrac{64}{3}x+\dfrac{179}{3}\)
d. Ta có : \(\dfrac{3}{\left(x_o+2\right)^2}=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}x_o+2=3\\x_o+2=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_o=1\\x_o=-5\end{matrix}\right.\)
Với xo = 1 \(\Rightarrow y_o=0\) . PTTT d : y = 1/3(x-1) = 1/3x - 1/3
Với xo = -5 \(\Rightarrow y_o=2\) . PTTT d : \(y=\dfrac{1}{3}\left(x+5\right)+2=\dfrac{1}{3}x+\dfrac{11}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2022
Theo tính chất hình lập phương, ta có:
\(C'D'\perp\left(BB'C'C\right)\Rightarrow C'D'\perp BC'\)
\(\Rightarrow\widehat{\left(C'D';BC'\right)}=90^0\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
\(\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)\)
Nếu \(a\ne1\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=a-1\ne0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=\infty\) ko thỏa mãn giả thiết \(=4\) (hữu hạn)
\(\Rightarrow a=1\)
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=-\dfrac{b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
\(y'=\left(3x^2\right)'-\left(4x\right)'+9'\)
\(y'=6x-4\Rightarrow y'\left(1\right)=6.1-4=2\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)
\(f\left(1\right)=m^2-15\)
Hàm liên tục tại \(x=1\) khi:
\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
\(4^2+\left(-3\right)^2=25\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=3x^2-2\)
hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)
\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)
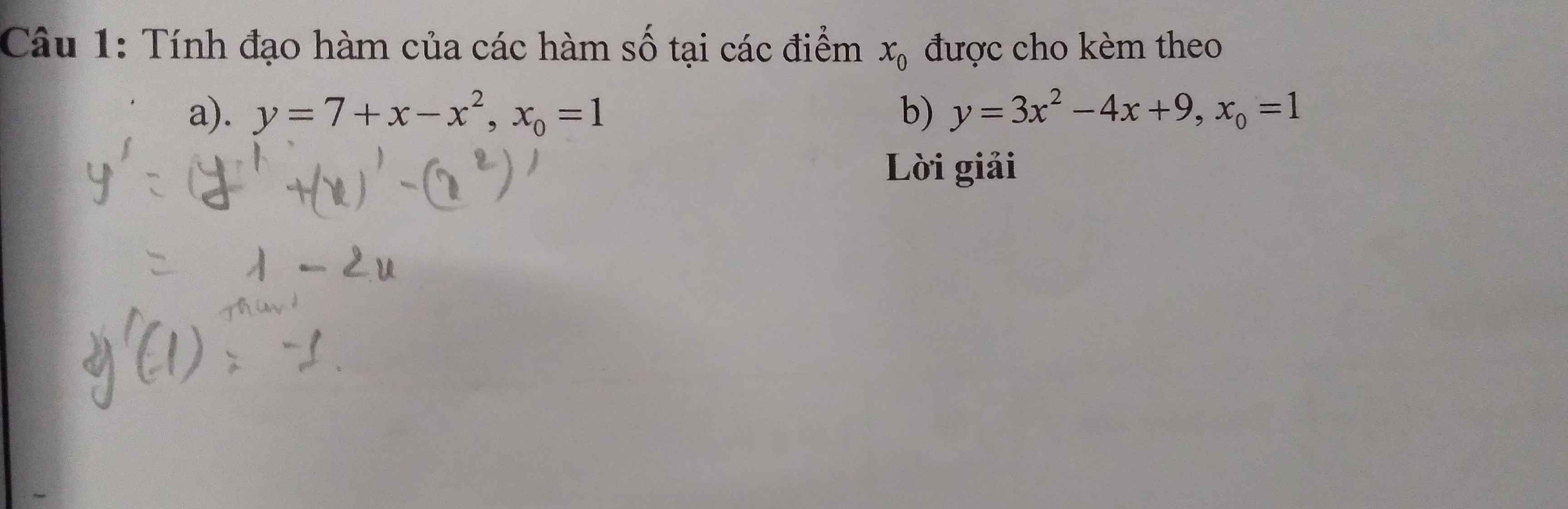
\(\left\{{}\begin{matrix}u_3=13\\u_5=23\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1+2d=13\\u_1+4d=23\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=3\\d=5\end{matrix}\right.\)