Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a-b+c}{2-3+5}=\dfrac{-10.2}{4}=-2.55\)
Do đó: a=-5,1; b=-7,65; c=-12,75

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)

\(\dfrac{x}{y}=\dfrac{5}{2}\) ⇒\(\dfrac{x}{5}=\dfrac{y}{2}\)
\(\dfrac{y}{z}=\dfrac{1}{3}\) ⇒\(\dfrac{y}{1}=\dfrac{z}{3}\) ⇒\(\dfrac{y}{2}=\dfrac{z}{6}\)
⇒\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{z}{6}\) ⇒\(\dfrac{x^2}{25}=\dfrac{y^2}{4}=\dfrac{2z^2}{72}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x^2}{25}=\dfrac{y^2}{4}=\dfrac{2z^2}{72}=\dfrac{x^2-y^2+2z^2}{25-4+72}=\dfrac{372}{93}=4\)
⇒\(\left\{{}\begin{matrix}x=4.5=20\\y=4.2=8\\z=4.6=24\end{matrix}\right.\)


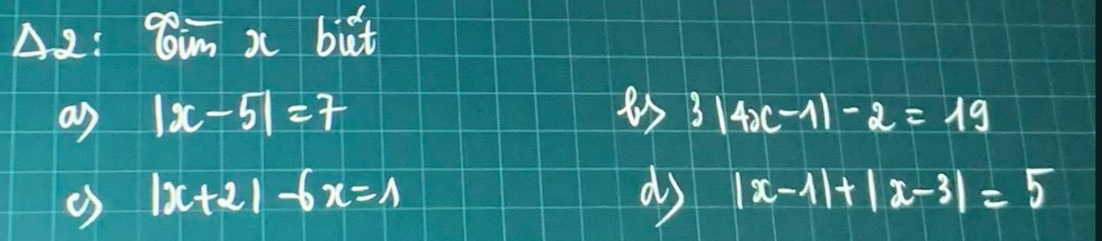 giúp em 4 câu này nhanh với ạ e cảm ơn
giúp em 4 câu này nhanh với ạ e cảm ơn
 Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ
Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ

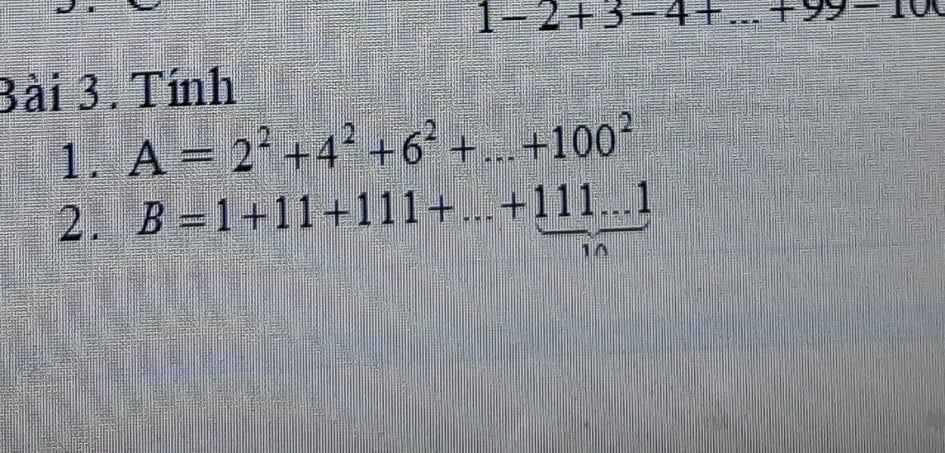 mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em câu a với ạ <33 em cảm ơn
Bài 4:
a: k=y/x=7/10
b: y=7/10x
c: Khi x=-6 thì y=-7/10*6=-42/10=-21/5
Khi x=1/7 thì y=1/7*7/10=1/10