K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
30.
\(y'=\dfrac{\left(x-2\right)'\left(x+2\right)-\left(x+2\right)'\left(x-2\right)}{\left(x+2\right)^2}=\dfrac{x+2-\left(x-2\right)}{\left(x+2\right)^2}=\dfrac{4}{\left(x+2\right)^2}\)
27.
D sai.
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc mặt đáy (trong khi D là "không vuông góc")
HP
9 tháng 12 2021
38.
Gọi T là biến cố "Trong 3 lần bắn, xạ thủ bắn trúng bia ít nhất 1 lần".
\(\Rightarrow\overline{T}\) là biến cố "Trong 3 lần bắn, xạ thủ không bắn trúng bia phát nào".
\(\Rightarrow P\left(\overline{T}\right)=0,4.0,4.0,4=0,064\)
\(\Rightarrow P\left(T\right)=1-P\left(\overline{T}\right)=0,936\)
HP
9 tháng 12 2021
37.
Ta đi tìm số các số tự nhiên lẻ có 5 chữ số đôi một khác nhau lập từ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Số tự nhiên có 5 chữ số có dạng \(\overline{abcde}\).
e có 5 cách chọn.
\(\overline{abcd}\) có \(A^4_9-A^3_8\) cách lập.
\(\Rightarrow\) Lập được \(5\left(A^4_9-A^3_8\right)\) số tự nhiên lẻ có 5 chữ số đôi một khác nhau.
\(\Rightarrow\) Lập được \(\left(A^5_{10}-A^4_9\right)-5\left(A^4_9-A^3_8\right)=13776\) số tự nhiên chẵn có 5 chữ số thỏa mãn yêu cầu bài toán.
17 tháng 10 2021
Chọn A.
\(2sin^2x-cosx+1=0\Rightarrow2\cdot\dfrac{1-cos2x}{2}-cosx+1=0\)
\(\Rightarrow1-\left(2cos^2x-1\right)-cosx+1=0\)
\(\Rightarrow-2cos^2x-cosx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{3}{2}\left(loại\right)\end{matrix}\right.\)\(\Rightarrow x=k2\pi\)
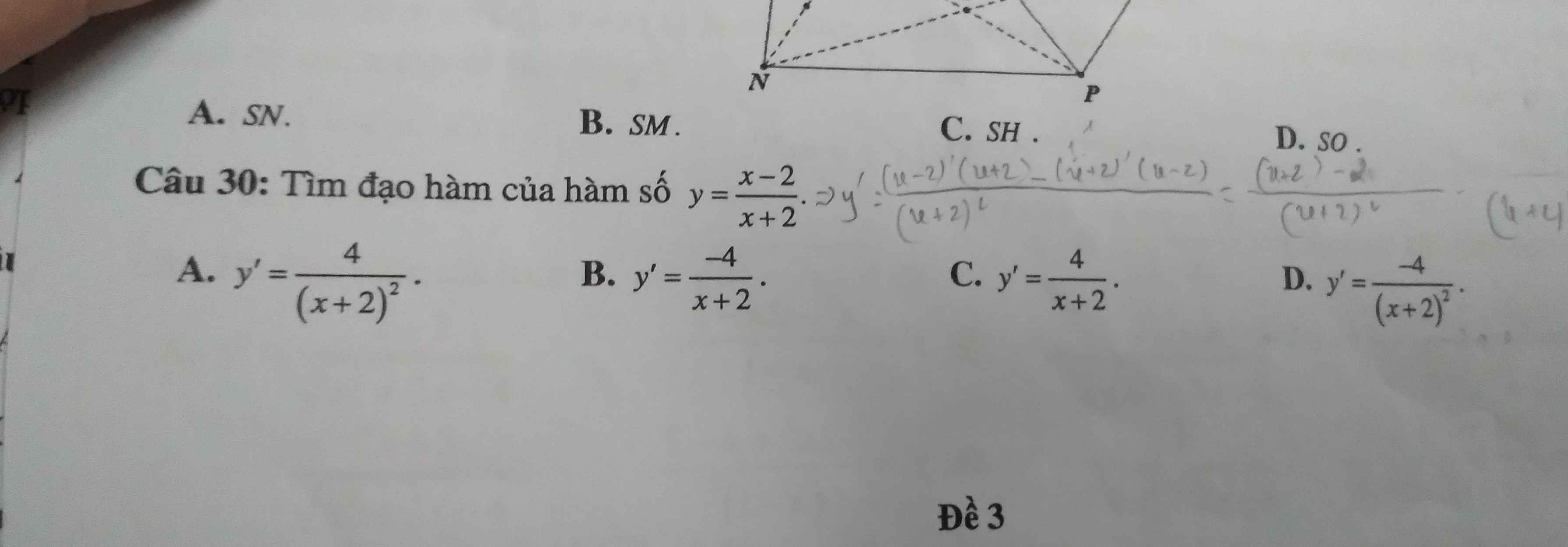
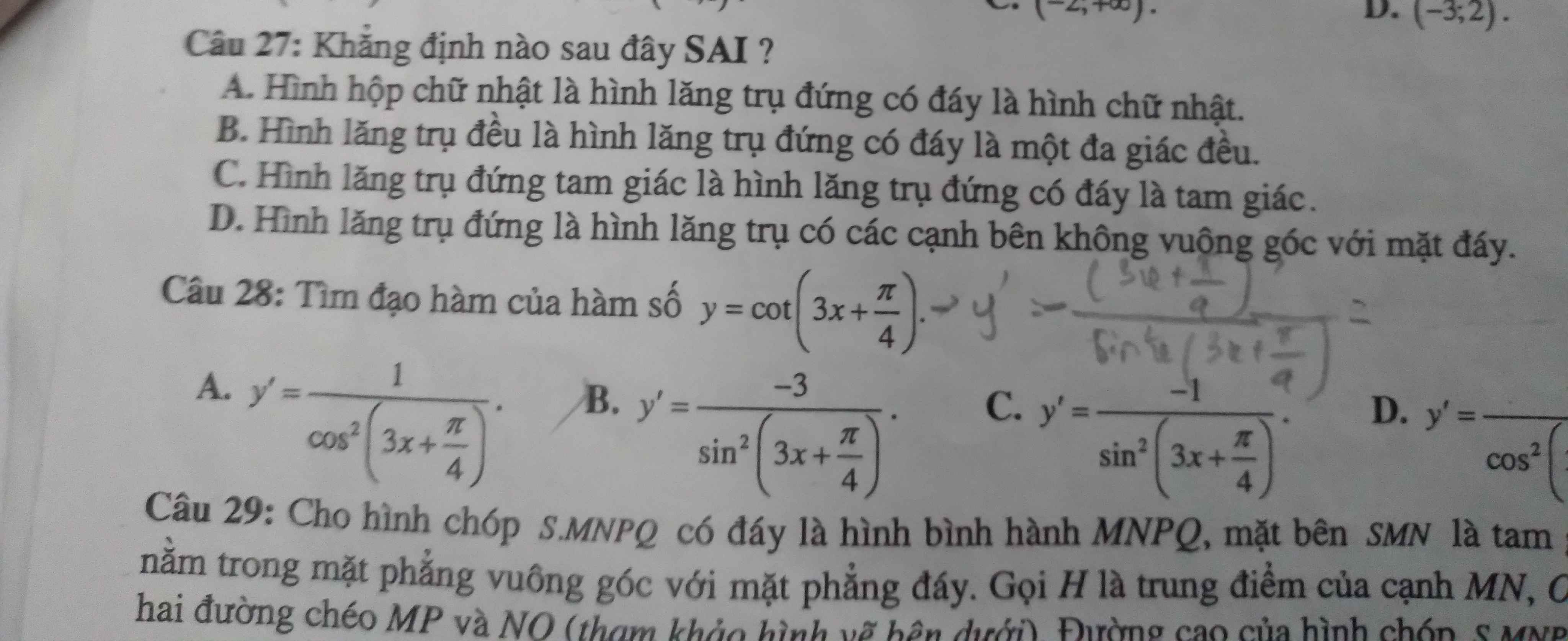
Nếu \(n\ne1\) ta có:
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+mx+8}+nx\right)=\lim\limits_{x\rightarrow-\infty}x\left(-\sqrt{1+\dfrac{m}{x}+\dfrac{8}{x^2}}+n\right)=-\infty.\left(n-1\right)=\infty\) không phải 1 giá trị hữu hạn (ktm)
\(\Rightarrow n=1\)
Khi đó:
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+mx+8}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{mx+8}{\sqrt{x^2+mx+8}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{m+\dfrac{8}{x}}{-\sqrt{1+\dfrac{m}{x}+\dfrac{8}{x^2}}-1}=\dfrac{m}{-2}=-\dfrac{m}{2}=4\)
\(\Rightarrow m=-8\)
\(\Rightarrow m+n=-8+1=-7\)