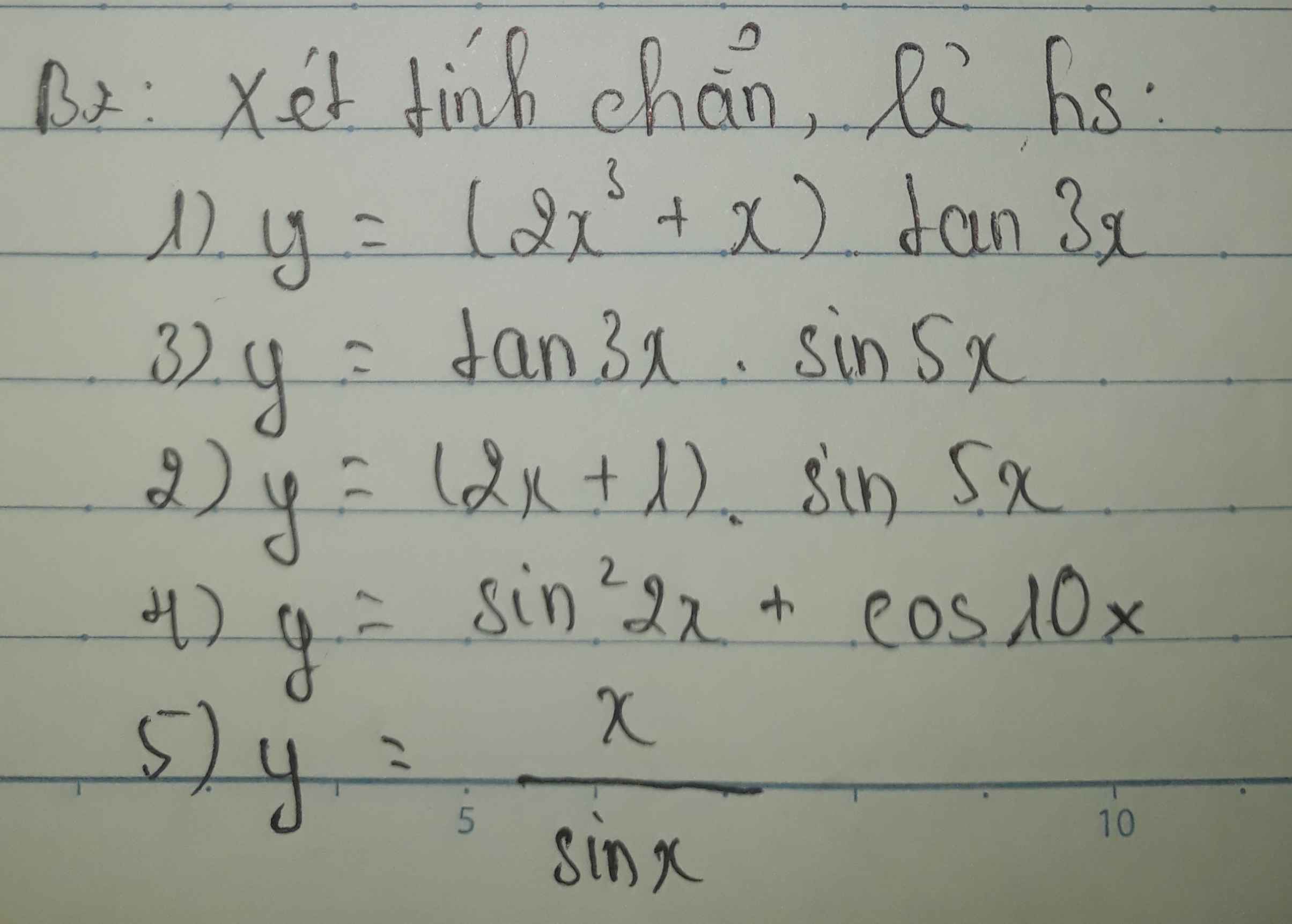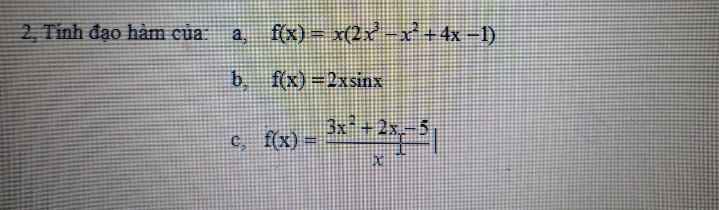K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
NT
0
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
Theo công thức tọa độ phép tịnh tiến:
a. \(\left\{{}\begin{matrix}x_{A'}=x_A+2=3+2=5\\y_{A'}=y_A+5=1+5=6\end{matrix}\right.\) \(\Rightarrow A'\left(5;6\right)\)
b. \(\left\{{}\begin{matrix}x_B=x_B'-1\\y_B=y_{B'}+3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_{B'}=x_B+1=5\\y_{B'}=y_B-3=-1\end{matrix}\right.\) \(\Rightarrow B'\left(5;-1\right)\)
c. \(\Delta'\) là ảnh của \(\Delta\) qua phép tịnh tiến nên \(\Delta'\) cùng phương \(\Delta\)
\(\Rightarrow\) Phương trình \(\Delta'\) có dạng: \(3x+y+c=0\) (1)
Lấy \(C\left(0;1\right)\in\Delta\), gọi \(T_{\overrightarrow{a}}\left(C\right)=C'\Rightarrow C'\in\Delta'\)
\(\left\{{}\begin{matrix}x_{C'}=x_C-1=-1\\y_{C'}=y_C+3=4\end{matrix}\right.\) \(\Rightarrow C'\left(-1;4\right)\)
Thế tọa độ C' vào (1):
\(-3+4+c=0\Rightarrow c=-1\)
Vậy pt \(\Delta'\) có dạng: \(3x+y-1=0\)
//Cách khác câu c:
Do pt \(\Delta\) dạng \(3x+y-1=0\) nên \(\Delta\) nhận \(\overrightarrow{u}=\left(-1;3\right)\) là 1 vtcp
Mà \(\overrightarrow{u}=\overrightarrow{a}\) hay \(\overrightarrow{u}\) và \(\overrightarrow{a}\) cùng phương nên \(\Delta'\) trùng \(\Delta\)
hay pt \(\Delta'\) có dạng: \(3x+y-1=0\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
d.
Đường tròn (C) tâm I(-1;3) bán kính R=2
\(\Rightarrow\) (C') có tâm \(I'\) sao cho \(T_{\overrightarrow{v}}\left(I\right)=I'\) và bán kính \(R'=R=2\)
\(\left\{{}\begin{matrix}x_{I'}=x_I+2=1\\y_{I'}=y_I+5=8\end{matrix}\right.\)
\(\Rightarrow I'\left(1;8\right)\)
Phương trình (C'):
\(\left(x-1\right)^2+\left(y-8\right)^2=4\)
HP
29 tháng 7 2021
a, \(f\left(x\right)=2x^4-x^3+4x^2-x\)
\(\Rightarrow f'\left(x\right)=\left(2x^4-x^3+4x^2-x\right)'\)
\(=\left(2x^4\right)'-\left(x^3\right)'+\left(4x^2\right)'-\left(x\right)'\)
\(=2.4x^3-3x^2+4.2x-1\)
\(=8x^3-3x^2+8x-1\)
b, \(f\left(x\right)=2sinx\)
\(\Rightarrow f'\left(x\right)=\left(2sinx\right)'=2cosx\)
c, \(f\left(x\right)=\dfrac{3x^2+2x-5}{x}\)
\(\Rightarrow f'\left(x\right)=\left(\dfrac{3x^2+2x-5}{x}\right)'\)
\(=\left(3x+2-\dfrac{5}{x}\right)'\)
\(=\left(3x\right)'+\left(2\right)'-\left(\dfrac{5}{x}\right)'\)
\(=3+0+\dfrac{5}{x^2}=\dfrac{5}{x^2}+3\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2022
\(\lim\dfrac{\left(3n^2+1\right)\left(1-4n\right)}{n^3-2n+5}=\lim\dfrac{\left(3+\dfrac{1}{n^2}\right)\left(\dfrac{1}{n}-4\right)}{1-\dfrac{2}{n^2}+\dfrac{5}{n^3}}=\dfrac{3.\left(-4\right)}{1}=-12\)
\(\lim\dfrac{\sqrt[]{4n^2-1}+\sqrt[]{n^2-5}}{n+\sqrt[3]{n^3-2n^2}}=\lim\dfrac{\sqrt[]{4-\dfrac{1}{n^2}}+\sqrt[]{1-\dfrac{5}{n^2}}}{1+\sqrt[3]{1-\dfrac{2}{n}}}=\dfrac{\sqrt[]{4}+\sqrt[]{1}}{1+\sqrt[3]{1}}=\dfrac{5}{2}\)
\(\lim\dfrac{\left(3-n\right)^7\left(2+n\right)^3}{\left(n^2+1\right)\left(n^8+3\right)}=\lim\dfrac{\left(\dfrac{3}{n}-1\right)^7\left(\dfrac{2}{n}+1\right)^3}{\left(1+\dfrac{1}{n^2}\right)\left(1+\dfrac{3}{n^8}\right)}=\dfrac{\left(-1\right)^7.1^3}{1.1}=-1\)
