K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BB
1
6 tháng 1 2023
Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2
VH
1
5 tháng 4 2022
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=3.6\left(cm\right)\)
CH=BC-BH=6,4(cm)
23 tháng 2 2022
a: Xét ΔOAD và ΔOCB có
OA/OC=3/6=OD/OB=2/4
góc AOD chung
Do đó:ΔOAD∼ΔOCB
b: Ta có: ΔOAD∼ΔOCB
=>OA/OC=AD/BC
=>1/2=4/BC
=>BC=8(cm)
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
4 tháng 1 2022
a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)
28 tháng 1 2023
a: Xét tứ giác MBQC có
N la trung điểm chung của MQ và BC
=>MBQC là hình bình hành
b: Xet tứ giácc AMQC có
AM//QC
AM=QC
góc MAC=90 độ
=>AMQC là hình chữ nhật
c: Xét ΔBAC có
N là trung điểm của CB
NK//AB
=>K là trung điểm của AC
Xét ΔCAB có
AN,BK,CM là các trung tuyến
nên ba đường này sẽ đồng quy
=>B,H,K thẳng hàng
3 tháng 1 2022
Bài 1:
a: =5(x+2y)
b: =(x+y)(5x-7)
Bài 2:
a: \(=\dfrac{1+2}{xy}=\dfrac{3}{xy}\)
NH
29 tháng 1 2023
a)
\(=\left(\dfrac{x}{x+3}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{1}{x}\right)\)
\(=\left(\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2+9}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{3x+1}{x\left(x-3\right)}-\dfrac{x-3}{x\left(x-3\right)}\right)\)
\(=\left(\dfrac{x^2-3x-x^2-9}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{3x+1-x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{-3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}:\dfrac{2x+4}{x\left(x-3\right)}\)
\(=\dfrac{-3}{\left(x-3\right)}\cdot\dfrac{x\left(x-3\right)}{2x+4}\\ =\dfrac{-3x}{2x+4}\)
b)
với `x=-1/2` (tmđk) ta có
\(\dfrac{-3\cdot\left(\dfrac{-1}{2}\right)}{2\cdot\left(-\dfrac{1}{2}\right)+4}=\dfrac{1}{2}\)
c)
để P=x thì
\(\dfrac{-3x}{2x+4}=x\)
\(=>-3x=\left(2x+4\right)\cdot x\)
\(-3x=2x^2+4x\)
\(2x^2+4x+3x=0\)
\(2x^2+7x=0\)
\(x\left(2x+7\right)=0\)
\(=>\left[{}\begin{matrix}x=0\\2x+7=0\end{matrix}\right.=>\left[{}\begin{matrix}x=0\left(loại\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
d)
mik ko bt lm=)
giúp mình bài này với ạ,từng bước lun nhé,mình cảm ơn ạ
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2022
\(15x^2y^5-10x^3y^4=5x^2y^4\left(3y-2x\right)\)
\(4x\left(x-2y\right)+7\left(2y-x\right)=4x\left(x-2y\right)-7\left(x-2y\right)=\left(x-2y\right)\left(4x-7\right)\)
\(5x^3+20x^2y+20xy^2=5x\left(x^2+4xy+4y^2\right)=5x\left(x+2y\right)^2\)
\(x^2-4y^2-2x+4y=\left(x-2y\right)\left(x+2y\right)-2\left(x-2y\right)=\left(x-2y\right)\left(x+2y-2\right)\)
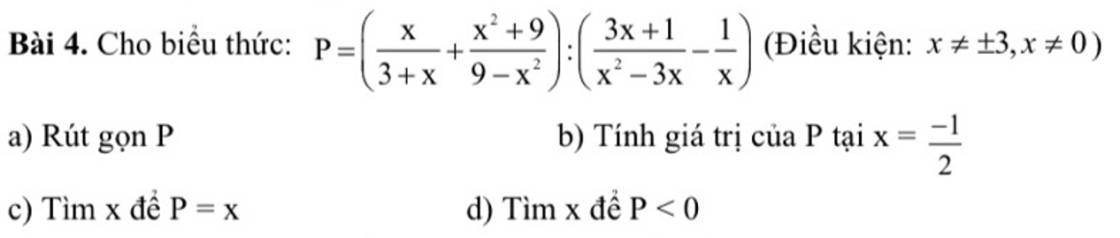
Sau khi giảm \(15\%\) thì giá mới là \(500000-500000\cdot15\%=4250000\left(đồng\right)\)