Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
Không gian mẫu: \(6.6=36\)
a.
Lần thứ nhất có 1 khả năng thỏa mãn (3 chấm)
Lần thứ 2 bất kì => có 6 khả năng
\(\Rightarrow1.6=6\) khả năng để lần thứ nhất xuất hiện mặt 3 chấm
Xác suất: \(P=\dfrac{6}{36}=\dfrac{1}{6}\)
b.
Xác suất để cả 2 lần đều ko xuất hiện mặt 2 chấm là: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất để ít nhất 1 lần xuất hiện mặt 2 chấm: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
c.
Các trường hợp có số chấm thuận lợi: (1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(3;1);(3;2);(4;1) có 10 trường hợp
Xác suất: \(P=\dfrac{10}{36}=\dfrac{5}{18}\)
Thầy có thể giải thích hơn về câu a và câu b của bài này được không ạ?
Số phần tử của không gian mẫu là: `n(Ω)=6`
A: "Số chấm xuất hiện nhỏ hơn ba"
`-> n(A)= 2`
`=> P(A)=(n(Ω))/(n(A))=2/6=1/3`
`=>` A.
Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với 
⇒ 
⇒ 
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
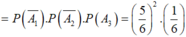
Đáp án B
Phương pháp: Xác suất của biến cố A là n A n Ω trong đó nA là số khả năng mà biến cố A có thể xảy ra, n Ω là tất cả các khả năng có thể xảy ra.
Cách giải: x 2 + b x + c x + 1 = 0 (*)
Để phương trình (*) vô nghiệm thì phương trình x2 + bx + c = 0 (**) có 2 trường hợp xảy ra:
TH1: PT (**) có 1 nghiệm x = -1
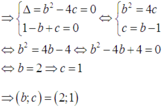
TH2: PT (**) vô nghiệm
Vì c là số chấm xuất hiện ở lần gieo thứ 2 nên c ≤ 6 ⇒ b ≤ 2 6 ≈ 4 , 9 .
Mà b là số chấm xuất hiện ở lần giao đầu nên b ∈ 1 ; 2 ; 3 ; 4
Với b = 1 ta có: c > 1 4 ⇒ c ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 có 6 cách chọn c.
Với b = 2 ta có: c > 1 ⇒ c ∈ 2 ; 3 ; 4 ; 5 ; 6 có 5 cách chọn c.
Với b = 3 ta có: c > 9 4 ⇒ c ∈ 3 ; 4 ; 5 ; 6 có 4 cách chọn c.
Với b = 4 ta có: c > 4 => c ∈ 5 ; 6 có 2 cách chọn c.
Do đó có 6+5+4+2 = 17 cách chọn (b;c) để phương trình (**) vô nghiệm.
Gieo con súc sắc 2 lần nên số phần tử của không gian mẫu n Ω = 6 . 6 = 36
Vậy xác suất đề phương trình (*) vô nghiệm là 1 + 17 36 = 1 2
Chọn C
Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp”
Biến cố A: “ số a b c ¯ chia hết cho 45”
a b c ¯ chia hết cho 45 ⇔ a b c ¯ chia hết cho cả 5 và 9
Vì a b c ¯ chia hết cho 5 nên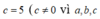
là số chấm xuất hiện của súc sắc khi gieo).
Vì a b c ¯ chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.
Các cặp số (a;b) sao cho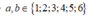
mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
Do đó: n(A) = 3.