K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 11 2021
\(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ Q=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)^2}{x}\)
28 tháng 5 2022
Câu 2:
Ta có: \(x^3+3x^2-4x-12=0\)
\(\Leftrightarrow x^2\left(x+3\right)-4\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
hay \(x\in\left\{-3;2;-2\right\}\)
LL
4 tháng 6 2021
gọi x là vận tốc của ô tô
y là vận tốc của xe máy (km/h) (x>y>0)
sau 4h 2 xe gặp nhau nên tổng quãng đường AB bằng:
AB= 4.x+4.y = 4.(x+y) (km)
nên thgian ô tô và xe máy đi hết AB lần lượt là:
\(\dfrac{4\left(x+y\right)}{y}\)(h); \(\dfrac{4\left(x+y\right)}{x}\) (h)
vì ô tô đến sớm hơn xe máy 6h nên ta có pt:
\(\dfrac{4\left(x+y\right)}{y}\)-\(\dfrac{4\left(x+y\right)}{x}\)=6
⇔\(\dfrac{4x+4y}{y}\)-\(\dfrac{4x+4y}{x}\)=6
⇔4.\(\dfrac{x}{y}\) +4-4-\(\dfrac{4y}{x}\)=6
⇔\(\dfrac{x}{y}\)-\(\dfrac{y}{x}\)=\(\dfrac{6}{4}\)=\(\dfrac{3}{2}\)
đặt: t=\(\dfrac{x}{y}\) (t>0)
⇒t-\(\dfrac{1}{t}\)=\(\dfrac{3}{2}\)
⇔t2-\(\dfrac{3}{2}\)t-1=0
⇔(t -2)(t +\(\dfrac{1}{2}\))=0
⇔t=2
⇒\(\dfrac{x}{y}\)=2 ⇒x=2y
⇒AB=4.(x+y)=6x=12y
nên thgian ô tô và xe máy đi hết AB lần lượt là:
\(\dfrac{6x}{x}=6\) (h)\(\dfrac{12y}{y}=12\) (h)
5 tháng 6 2021
Gọi thời gian xe máy đi hết quãng đường AB là x (h) (x>4)
thời gian xe máy đi hết quãng đường AB là y (h) (y>4)
Trong 1 giờ xe máy đi được \(\dfrac{1}{x}\) (quãng đường)
Trong 1 giờ ô tô đi được \(\dfrac{1}{y}\) (quãng đường)
Trong 1 giờ hai xe đi được \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Mà thời gian ô tô về đến A sớm hơn xe máy về đến B là 6 giờ nên: \(x-y=6\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\x-y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{x-6}=\dfrac{1}{4}\\y=x-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-14x+24=0\\y=2-6\end{matrix}\right.\)(ĐK:\(x\ne6\)) \(\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\)(TM)
Vậy thời gian xe máy đi hết quãng đường AB là 12 giờ
thời gian ô tô đi hết quãng đường AB là 6giờ
-Chúc bạn học tốt-
NC
2
9 tháng 11 2021
1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)
NH
1
31 tháng 8 2021
Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
Y
29 tháng 6 2023
\(1,2\sqrt{27}+5\sqrt{12}-3\sqrt{48}\\ =2.3\sqrt{3}+5.2\sqrt{3}-3.4\sqrt{3}\\ =6\sqrt{3}+10\sqrt{3}-12\sqrt{3}\\ =4\sqrt{3}\)
\(2,\sqrt{147}+\sqrt{75}-4\sqrt{27}\\ =7\sqrt{3}+5\sqrt{3}-4.3\sqrt{3}\\ =7\sqrt{3}+5\sqrt{3}-12\sqrt{3}\\ =\sqrt{3}\left(7+5-12\right)\\ =0\)
\(3,3\sqrt{2}\left(4-\sqrt{2}\right)+3\left(1-2\sqrt{2}\right)^2\\ =3\sqrt{2}.\left(4-\sqrt{2}\right)+3\left(1-4\sqrt{2}+8\right)\\ =12\sqrt{2}-6+3-12\sqrt{2}+24\\ =21\)
\(4,2\sqrt{5}-\sqrt{125}-\sqrt{80}+\sqrt{605}\\ =2\sqrt{5}-5\sqrt{5}-4\sqrt{5}+11\sqrt{5}\\ =\sqrt{5}\left(2-5-4+11\right)\\ =4\sqrt{5}\)
29 tháng 6 2023
1: =6căn 3+10căn 3-12căn 3=4căn 3
2: =7căn 3+5căn 3-12căn 3=0
3: =12căn 2-6+3(9-4căn 2)
=12căn 2-6+27-12căn 2=21
4: =2căn 5-5căn 5+4căn 5+9 căn 5
=10căn 5
DT
4
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
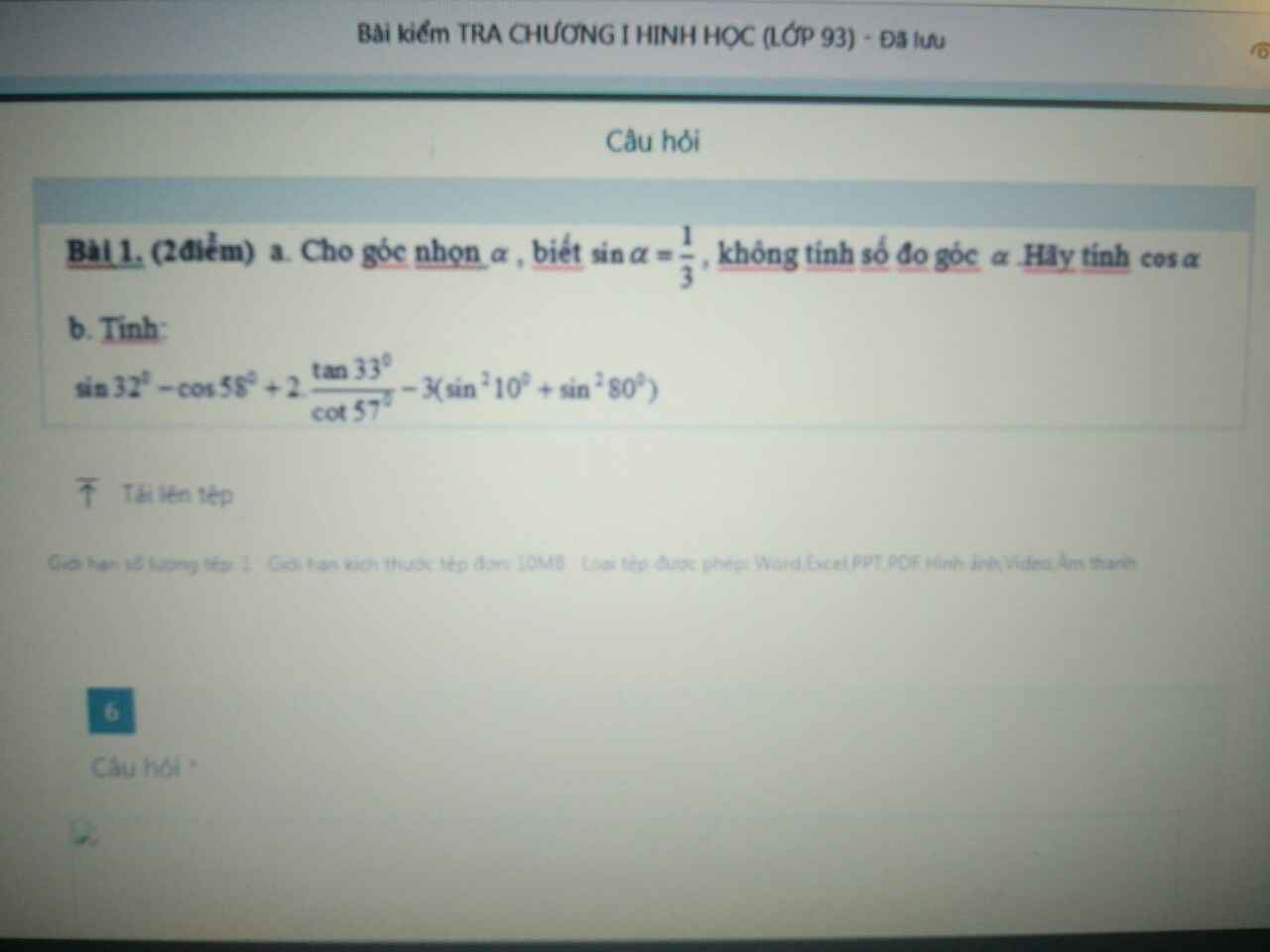
Bài 1:
a. $\sin ^2a+\cos ^2a=1$
$\cos ^2a=1-\sin ^2a=1-(\frac{1}{3})^2=\frac{8}{9}$
$\Rightarrow \cos a=\frac{2\sqrt{2}}{3}$ (do $\cos a>0$)
b.
\(\sin 32-\cos 58+2\frac{\tan 33}{\cot 57}-3(\sin ^210+\sin ^280)\)
\(=\cos (90-32)-\cos 58+2\frac{\tan 33}{\tan (90-57)}-3(\sin ^210+\cos ^2(90-80))\)
\(=\cos 58-\cos 58+2\frac{\tan 33}{\tan 33}-3(\sin ^210+\cos ^210)\)
\(=0+2.1-3.1=-1\)
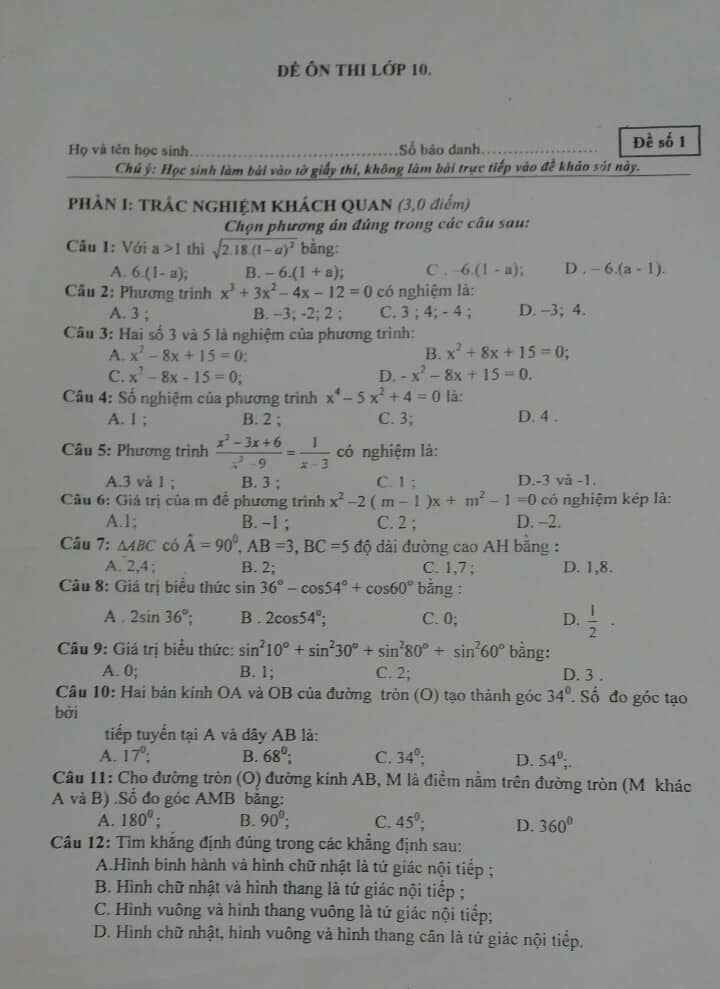
\(b,\text{PT }\left(d_1\right)\text{ giao Oy: }x=0\Leftrightarrow y=2\Leftrightarrow A\left(0;2\right)\\ \text{PT }\left(d_2\right)\text{ giao Oy: }x=0\Leftrightarrow y=-2\Leftrightarrow B\left(0;-2\right)\\ \text{PT hoành độ giao điểm }\left(d_1\right);\left(d_2\right):2x+2=-\dfrac{1}{2}x-2\\ \Leftrightarrow\dfrac{5}{2}x=-4\Leftrightarrow x=-\dfrac{8}{5}\Leftrightarrow y=-\dfrac{6}{5}\Leftrightarrow C\left(-\dfrac{8}{5};-\dfrac{6}{5}\right)\\ c,\text{Vì }2>0\text{ nên góc tạo đc là góc nhọn}\\ \text{Gọi góc đó là }\alpha\left(\alpha< 90\right)\\ \text{Ta có hs góc của }\left(d_1\right)\text{ là }2\\ \Leftrightarrow\tan\alpha=2\approx\tan63^026'\\ \Leftrightarrow\alpha\approx63^026'\)