Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
a, \(\left(C\right)x^2+y^2-6x-2y+6=0\)
\(\Leftrightarrow\left(C\right)\left(x-3\right)^2+\left(y-1\right)^2=4\)
\(\Rightarrow\) Tâm \(I=\left(3;1\right)\), bán kính \(R=2\)
b, Tiếp tuyến đi qua A có dạng: \(\left(\Delta\right)ax+by-5a-7b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|3a+b-5a-7b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+3b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow6ab+8b^2=0\)
\(\Leftrightarrow2b\left(3a+4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b=0\\3a+4b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
TH1: \(\Delta_1:x=5\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x=5\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y^2-2y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\Rightarrow\left(5;1\right)\)
TH2: \(\Delta_2:4x-3y+1=0\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}4x-3y+1=0\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{5}\\y=\dfrac{11}{5}\end{matrix}\right.\Rightarrow\left(\dfrac{7}{5};\dfrac{11}{5}\right)\)
Kết luận: Phương trình tiếp tuyến: \(\left\{{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
Tọa độ tiếp điểm: \(\left\{{}\begin{matrix}\left(5;1\right)\\\left(\dfrac{7}{5};\dfrac{11}{5}\right)\end{matrix}\right.\)

Câu 1: \(\overrightarrow{IA}+\overrightarrow{IB}=0\)
Bởi vì khi đó, IA và IB là hai vecto đối nhau
Suy ra: IA và IB là hai vecto cùng phương
mà IA và IB có điểm chung là I
nên A,I,B thẳng hàng và IA=IB
Suy ra: I là trung điểm của AB

Đồ thị hướng lên nên a > 0 => Loại A,B
Dựa vào đồ thị, A( 1; 0) thuộc đồ thị => Chọn C

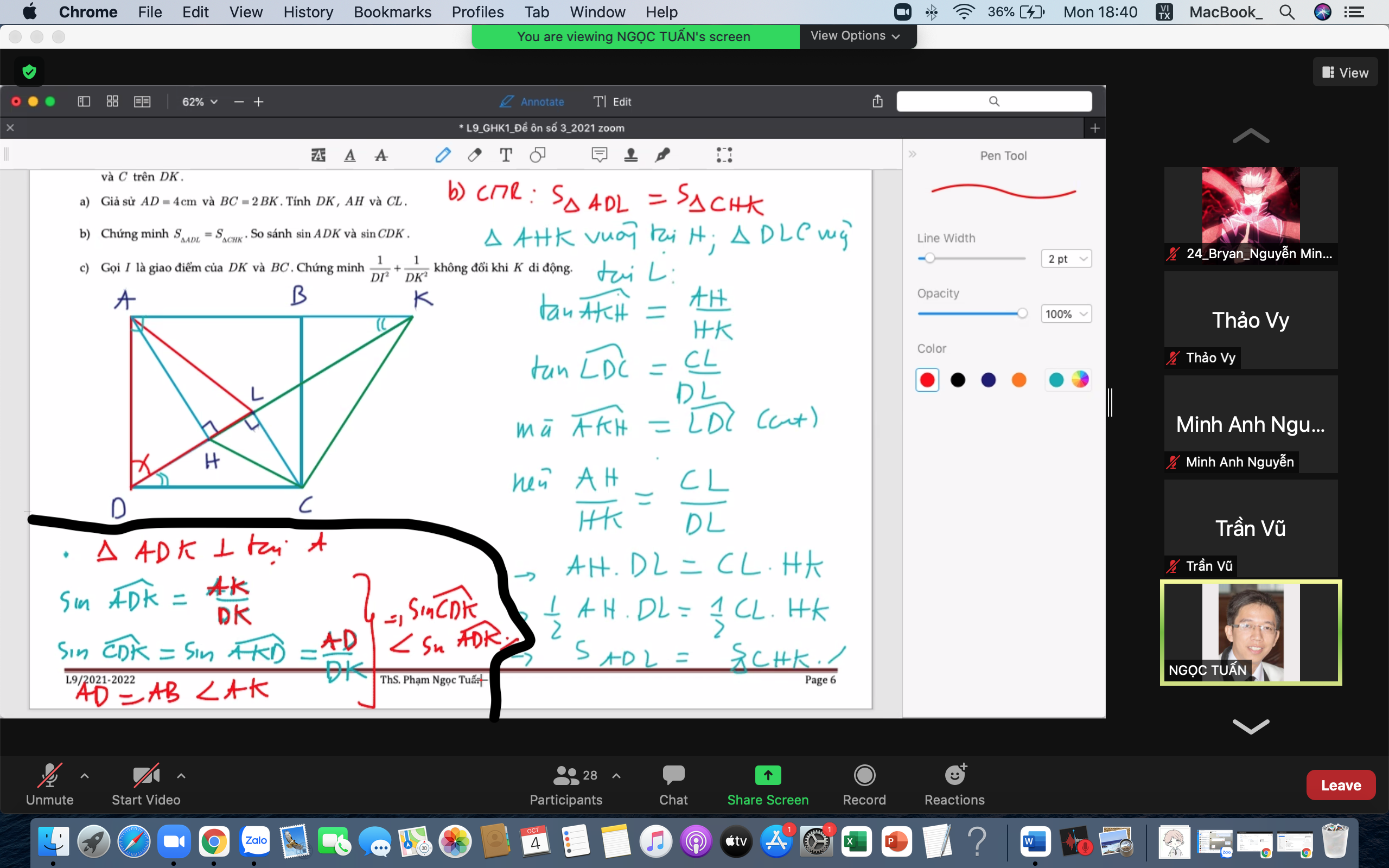

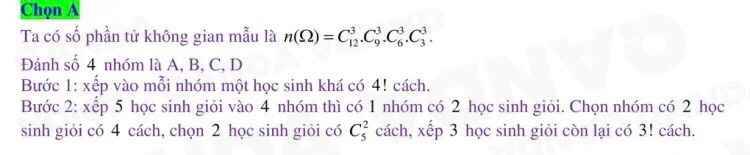








Chụp nốt cái đề để bt đề cho j đã chứ
Đề nè iem.