Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
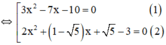
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
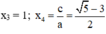
Vậy phương trình có tập nghiệm 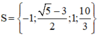
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
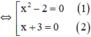
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
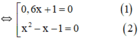
+ Giải (1): 0,6x + 1 = 0 ⇔ 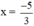
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 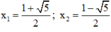
Vậy phương trình có tập nghiệm 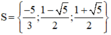
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
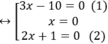
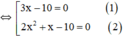
+ Giải (1): 3x – 10 = 0 ⇔ 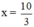
+ Giải (2):
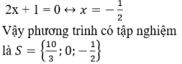

a)
3 · x 2 + x 2 - 2 x 2 + x - 1 = 0 ( 1 )
Đặt t = x 2 + x ,
Khi đó (1) trở thành : 3 t 2 – 2 t – 1 = 0 ( 2 )
Giải (2) : Có a = 3 ; b = -2 ; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 ; t 2 = c / a = - 1 / 3 .
+ Với t = 1 ⇒ x 2 + x = 1 ⇔ x 2 + x – 1 = 0 ( * )
Có a = 1; b = 1; c = -1 ⇒ Δ = 1 2 – 4 . 1 . ( - 1 ) = 5 > 0
(*) có hai nghiệm
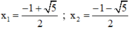
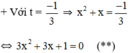
Có a = 3; b = 3; c = 1 ⇒ Δ = 3 2 – 4 . 3 . 1 = - 3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm 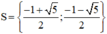
b)
x 2 − 4 x + 2 2 + x 2 − 4 x − 4 = 0 ⇔ x 2 − 4 x + 2 2 + x 2 − 4 x + 2 − 6 = 0 ( 1 )
Đặt x 2 – 4 x + 2 = t ,
Khi đó (1) trở thành: t 2 + t – 6 = 0 ( 2 )
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 1 2 – 4 . 1 . ( - 6 ) = 25 > 0
⇒ (2) có hai nghiệm
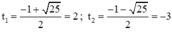
+ Với t = 2 ⇒ x 2 – 4 x + 2 = 2
⇔ x 2 – 4 x = 0
⇔ x(x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x 2 – 4 x + 2 = - 3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ ’ = ( - 2 ) 2 – 1 . 5 = - 1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
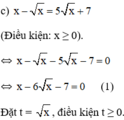
Khi đó (1) trở thành: t 2 – 6 t – 7 = 0 ( 2 )
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = 7 .
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
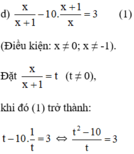
⇔ t 2 – 10 = 3 t ⇔ t 2 – 3 t – 10 = 0 ( 2 )
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = ( - 3 ) 2 - 4 . 1 . ( - 10 ) = 49 > 0
⇒ (2) có hai nghiệm:
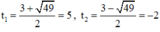
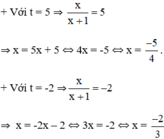
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm 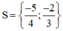

a) Phương trình bậc hai
2 x 2 – 7 x + 3 = 0
Có: a = 2; b = -7; c = 3;
Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 2 . 3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
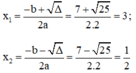
Vậy phương trình có hai nghiệm là 3 và 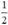
b) Phương trình bậc hai 6 x 2 + x + 5 = 0
Có a = 6; b = 1; c = 5;
Δ = b 2 – 4 a c = 12 – 4 . 5 . 6 = - 119 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 6 x 2 + x – 5 = 0
Có a = 6; b = 1; c = -5;
Δ = b 2 – 4 a c = 12 – 4 . 6 . ( - 5 ) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
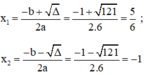
Vậy phương trình có hai nghiệm là -1 và 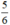
d) Phương trình bậc hai 3 x 2 + 5 x + 2 = 0
Có a = 3; b = 5; c = 2;
Δ = b 2 – 4 a c = 5 2 – 4 . 3 . 2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
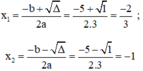
Vậy phương trình có hai nghiệm là -1 và 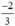
e) Phương trình bậc hai y 2 – 8 y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b 2 – 4 a c = ( - 8 ) 2 – 4 . 1 . 16 = 0 .
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
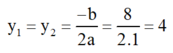
Vậy phương trình có nghiệm kép y = 4.
f) Phương trình bậc hai 16 z 2 + 24 z + 9 = 0
Có a = 16; b = 24; c = 9; Δ = b 2 – 4 a c = 24 2 – 4 . 16 . 9 = 0
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:
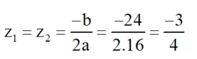
Vậy phương trình có nghiệm kép 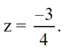
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 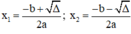
+ Nếu Δ = 0, phương trình có nghiệm kép 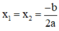 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

5x4 + 2x2 – 16 = 10 – x2
⇔ 5x4 + 2x2 – 16 – 10 + x2 = 0
⇔ 5x4 + 3x2 – 26 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 5t2 + 3t – 26 = 0 (2)
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 32 – 4.5.(-26) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
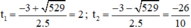
Đối chiếu điều kiện chỉ có t1 = 2 thỏa mãn
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}


a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
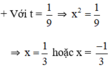
Vậy phương trình (1) có tập nghiệm 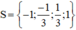
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
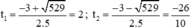
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
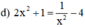
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
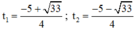
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
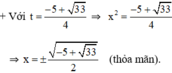
Vậy phương trình có tập nghiệm 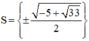
giup mình voi huhu
a) Đặt \(x^2=a\left(a\ge0\right)\)
Ta có: \(2x^4-7x^2+4=0\)
Suy ra: \(2a^2-7a+4=0\)
\(\Delta=49-4\cdot2\cdot4=49-32=17\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{7-\sqrt{17}}{4}\left(nhận\right)\\a_2=\dfrac{-7+\sqrt{17}}{4}\left(loại\right)\end{matrix}\right.\)
Suy ra: \(x^2=\dfrac{7-\sqrt{17}}{4}\)
\(\Leftrightarrow x=\pm\dfrac{\sqrt{7-\sqrt{17}}}{2}\)
Vậy: \(S=\left\{\dfrac{\sqrt{7-\sqrt{17}}}{2};-\dfrac{\sqrt{7-\sqrt{17}}}{2}\right\}\)