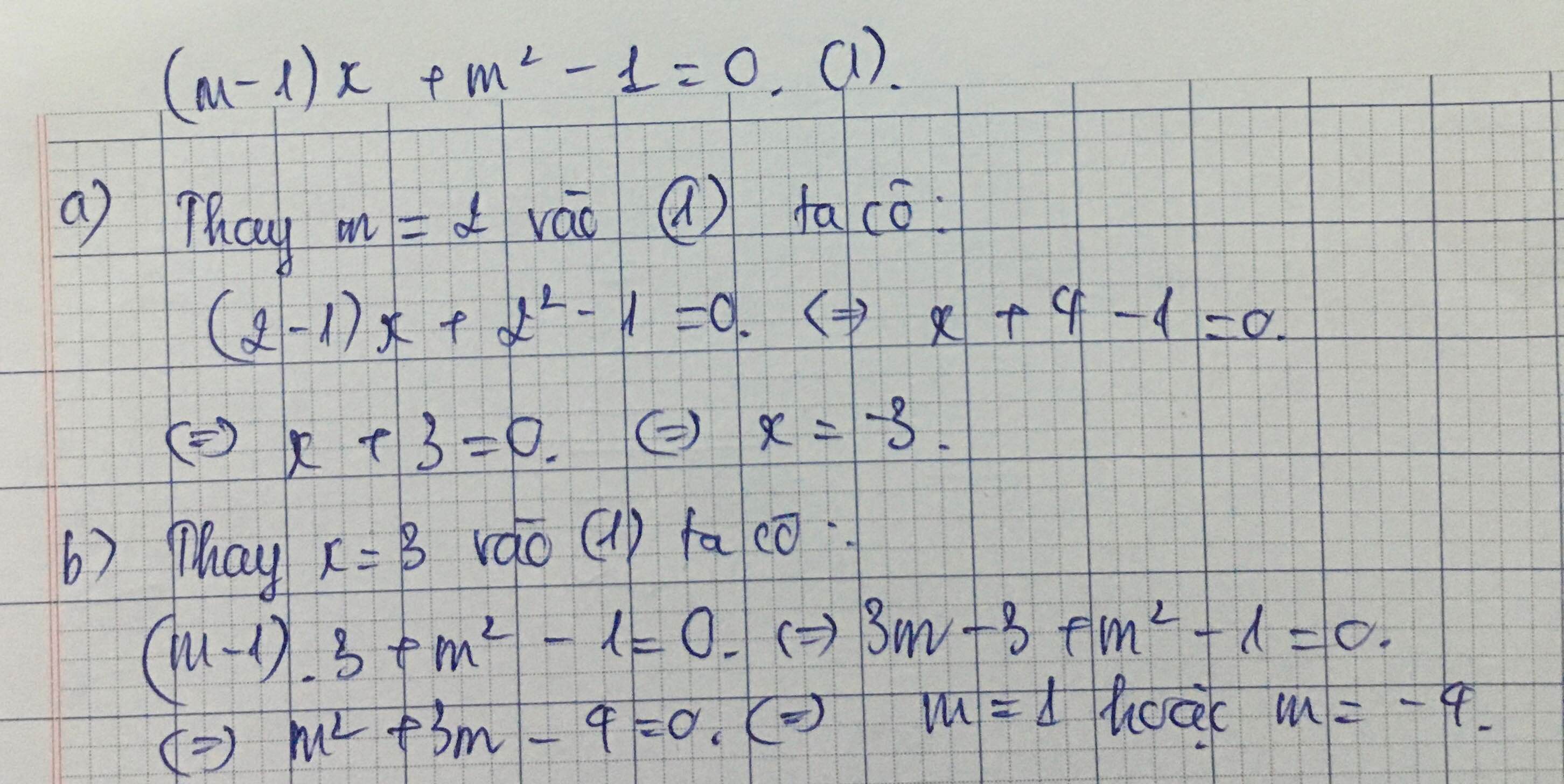K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QO
2
25 tháng 5 2018
a( ax + 1) = x( a + 2) + 2
⇔ a2x + a - ax- 2x = 2 - a
⇔ x( a2 - a - 2 ) = 2 - a
⇔ x( a2 + a - 2a - 2) = 2 - a
⇔ x[ a( a + 1) -2( a + 1) ] = 2 - a
⇔ x( a + 1)( a - 2) = 2 - a ( *)
+) Với : a # 2 ; a # - 1 , ta có :
( * ) ⇔ x = \(\dfrac{-1}{a+1}\)
+) Với : a = 2 , ta có :
( * ) ⇔ 0x= 0 ( Luôn đúng )
+) Với : a = - 1 , ta có :
( * ) ⇔0x = 3 ( Vô lý )
KL.....
25 tháng 5 2018
<=>(a^2-a-2)x=2-a
[(a-1/2)^2-(3/2)^2]x=2-a
<=>(a+1)(a-2)x=2-a
a=2 ; =>moi x$R
a=-1 ; vo nghiem
a≠{-1;2}: x=-1/(a+1)
MQ
27 tháng 3 2020
a, Ta có phương trình
(m-1)x=m^2 -1 => (m-1)x-m^2+1 =0 (1)
Vậy phương trình (1) là phương trình bậc nhất (=) (m-1) khác 0.
(=) m khác 1
b, Ta có phương trình (1)
(m-1)x - m2 +1 = 0 => mx -x -m2 +1 = 0
+) Nếu m=1 => phương trình (1) có dạng 0x = 0
+) Nếu m khác 1 => Ptrinh (1) có nghiệm là x=(1-m2)/(m-1)
Vậy với m=1 ptinh có S=R
với m khác 1 ptrinh có S={(1-m2)/(m-1)}
Chúc bạn học tốt
14 tháng 2 2018
a) Ta có: \(\frac{x+a}{x+2}+\frac{x-2}{x-a}=2\left(1\right)\)
Với a = 4
Thay vào phương trình (t) ta được:
\(\frac{x+2}{x+2}+\frac{x-2}{x-2}=2\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\frac{\left(x-2\right)\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\frac{2\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow x^2-4+x^2-4=2\left(x^2-4\right)\)
\(\Leftrightarrow2x^2=2x^2-8\)
\(\Leftrightarrow0x=-8\)
Vậy phương trình vô nghiệm
b) Nếu x = -1
\(\Rightarrow\frac{-1+a}{-1+2}+\frac{-1-2}{-1-a}=2\)
\(\Leftrightarrow\frac{-1+a}{1}+\frac{-3}{-1-a}=2\)
\(\Leftrightarrow\frac{\left(-1+a\right)\left(-1-a\right)}{-1-a}+\frac{-3}{-1-a}=\frac{2\left(-1-a\right)}{-1-a}\)
\(\Leftrightarrow1+a-a-a^2-3=-2-2a\)
\(\Leftrightarrow-a^2+2a=-2-1+3\)
\(\Leftrightarrow a\left(2-a\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=0\\2-a=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=0\\a=2\end{cases}}}\)
Vậy a = {0;2}
NĂM MỚI VUI VẺ
16 tháng 2 2020
b) \(\frac{10x+1}{7}=\frac{7x-2}{4}\)
<=> \(\frac{4\left(10x+1\right)}{28}=\frac{7\left(7x-2\right)}{28}\)
<=> 40x + 4 = 49x - 14
<=> 40x - 49x = -14 - 4
<=> -9x = -18
<=> x = 2
Vậy S = {2}
c) \(\frac{x-5}{5}-2=\frac{1+19x}{6}\)
<=> \(\frac{6\left(x-5\right)-60}{30}=\frac{5\left(1+19x\right)}{30}\)
<=> 6x - 30 - 60 = 5 + 95x
<=> 6x - 95x = 5 + 90
<=> -89x = 95
<=> x = -95/89
Vậy S = {-95/89}
DT
1
C
19 tháng 4 2017
ĐK: a \(\ne\) 0
BPT tương đương
x +\(\frac{x}{a}\)- \(\frac{1}{a}\)- \(\frac{x}{a}\)- \(\frac{1}{a}\)+ (a - 2)x < 0
<=> x - \(\frac{2}{a}\)+ (a - 2) x < 0
<=> (a - 1)x < \(\frac{2}{a}\)
TH1: a = 1: BPT luôn đúng với mọi x
TH2: a > 1: BPT tương đương:
x < \(\frac{2}{a\left(a-1\right)}\)
TH3: a < 1 (a\(\ne\)0) BPT tương đương:
x > \(\frac{2}{a\left(a-1\right)}\)
A
1
NT
1
19 tháng 2 2021
a)(3x-1)(4x-8)=0
⇔3x-1=0 hoặc 4x-8=0
1.3x-1=0⇔3x=1⇔x=1/3
2.4x-8=0⇔4x=8⇔x=2
phương trình có 2 nghiệm:x=1/3 và x=2
b)(x-2)(1-3x)=0
⇔x-2=0 hoặc 1-3x=0
1.x-2=0⇔x=2
2.1-3x=0⇔-3x=1⇔x=-1/3
phương trình có 2 nghiệm:x=2 và x=-1/3
c)(x-3)(x+4)-(x-3)(2x-1)=0
⇔(x+4)(2x-1)=0
⇔x+4=0 hoặc 2x-1=0
1.x+4=0⇔x=-4
2.2x-1=0⇔2x=1⇔x=1/2
phương trình có hai nghiệm:x=-4 và x=1/2
d)(x+1)(x+2)=2x(x+2)
⇔(x+1)(x+2)-2x(x+2)=0
⇔2x(x+1)=0
⇔2x=0 hoặc x+1=0
1.2x=0⇔x=0
2.x+1=0⇔x=-1
phương trình có 2 nghiệm:x=0 và x=-1
