Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

=>xy-2x=xy-4x+2y-8 và 2xy+7x-6y-21=2xy+6x-7y-21
=>2x-2y=-8 và x+y=0
=>x-y=-4 và x+y=0
=>2x=-4 và x+y=0
=>x=-2 và y=2

b: Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=0\)
\(\Leftrightarrow\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24=0\)
\(\Leftrightarrow x^2+7x+6=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-6\end{matrix}\right.\)

a) \(x^4-x^2+\dfrac{1}{4}-\dfrac{225}{4}=0\\ \left(x^2-\dfrac{1}{2}\right)^2-\dfrac{15}{2}^2=0\\ \left(x+7\right)\left(x-8\right)=0\\ \left[{}\begin{matrix}x=8\\x=-7\end{matrix}\right.\)
Vậy x = 8 hoặc x = -7
a: Ta có: \(x^4-x^2-56=0\)
\(\Leftrightarrow x^4-8x^2+7x^2-56=0\)
\(\Leftrightarrow\left(x^2-8\right)\left(x^2+7\right)=0\)
\(\Leftrightarrow x^2-8=0\)
hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)

a) Ta có: \(\left\{{}\begin{matrix}2\left(x+1\right)-3\left(y-2\right)=5\\-4\left(x-2\right)+5\left(y-3\right)=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2-3y+6=5\\-4x+8+5y-15=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-3\\-4x+5y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-6y=-6\\-4x+5y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=0\\2x-3y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x-3\cdot0=-3\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=0\end{matrix}\right.\)
Vậy: hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=0\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}8\left(x-3\right)-3\left(y+1\right)=-2\\3\left(x+2\right)-2\left(1-y\right)=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-24-3y-3=-2\\3x+6-2+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-3y=25\\3x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y=75\\24x+16y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-25y=67\\3x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-67}{25}\\3x=1-2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=1-2\cdot\dfrac{-67}{25}=\dfrac{159}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
a) HPT \(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-3\\-4x+5y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x-6y=-6\\-4x+5y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-y=0\\x=\dfrac{3y-3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(-\dfrac{3}{2};0\right)\)
b) HPT \(\Leftrightarrow\left\{{}\begin{matrix}8x-3y=25\\3x+2y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}16x-6y=50\\9x+6y=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}25x=53\\y=\dfrac{1-3x}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{53}{25}\\y=-\dfrac{67}{25}\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm \(\left(x;y\right)=\left(\dfrac{53}{25};-\dfrac{67}{25}\right)\)

\(\left(x-2\right)\left(x-1\right)\left(x-4\right)\left(x-8\right)=4x^2\)
\(\Leftrightarrow[\left(x-2\right)\left(x-4\right)][\left(x-1\right)\left(x-8\right)]=4x^2\)
\(\Leftrightarrow\left(x^2-6x+8\right)\left(x^2-9x+8\right)=4x^2\)
thấy \(x=0;2\) không phải nghiệm của phương trình nên ta chia hai vế của pt cho \(x^2\) ta được \(:\)
\(\Leftrightarrow\left(x+\dfrac{8}{x}-9\right)\left(x+\dfrac{8}{x}-6\right)=4\)
\(Đặt:\) \(x+\dfrac{8}{x}=a\) thì pt trở thành \(:\)
\(\left(a-6\right)\left(a-9\right)=4\)
\(\Leftrightarrow a^2-15a+50=0\)
\(\Leftrightarrow\left(a-5\right)\left(a-10\right)=0\Leftrightarrow\left\{{}\begin{matrix}a=5\\a=10\end{matrix}\right.\)
\(Với\) \(a=5\) thì \(x+\dfrac{8}{x}=5\Leftrightarrow x^2-5x+8=0\left(vônghiem\right)\)
\(Với\) \(a=10\) thì \(x+\dfrac{8}{x}=10\Leftrightarrow x^2-10x+8=0\Leftrightarrow\left\{{}\begin{matrix}x=5-căn17\\x=5+căn17\end{matrix}\right.\)
\(Vậy...\)

đề <=> \(\left(x^2+2x\right)\left(x^2+2x-8\right)\)\(=-7\) (1)
đặt x2+2x-4=a
từ (1) => (a-4)(a+4)= -7
<=> a2-16=-7
<=> a2-9=0
<=>(a-3)(a+3)=0
=> a=3 hoặc a=-3
thay số vào làm nốt nhé
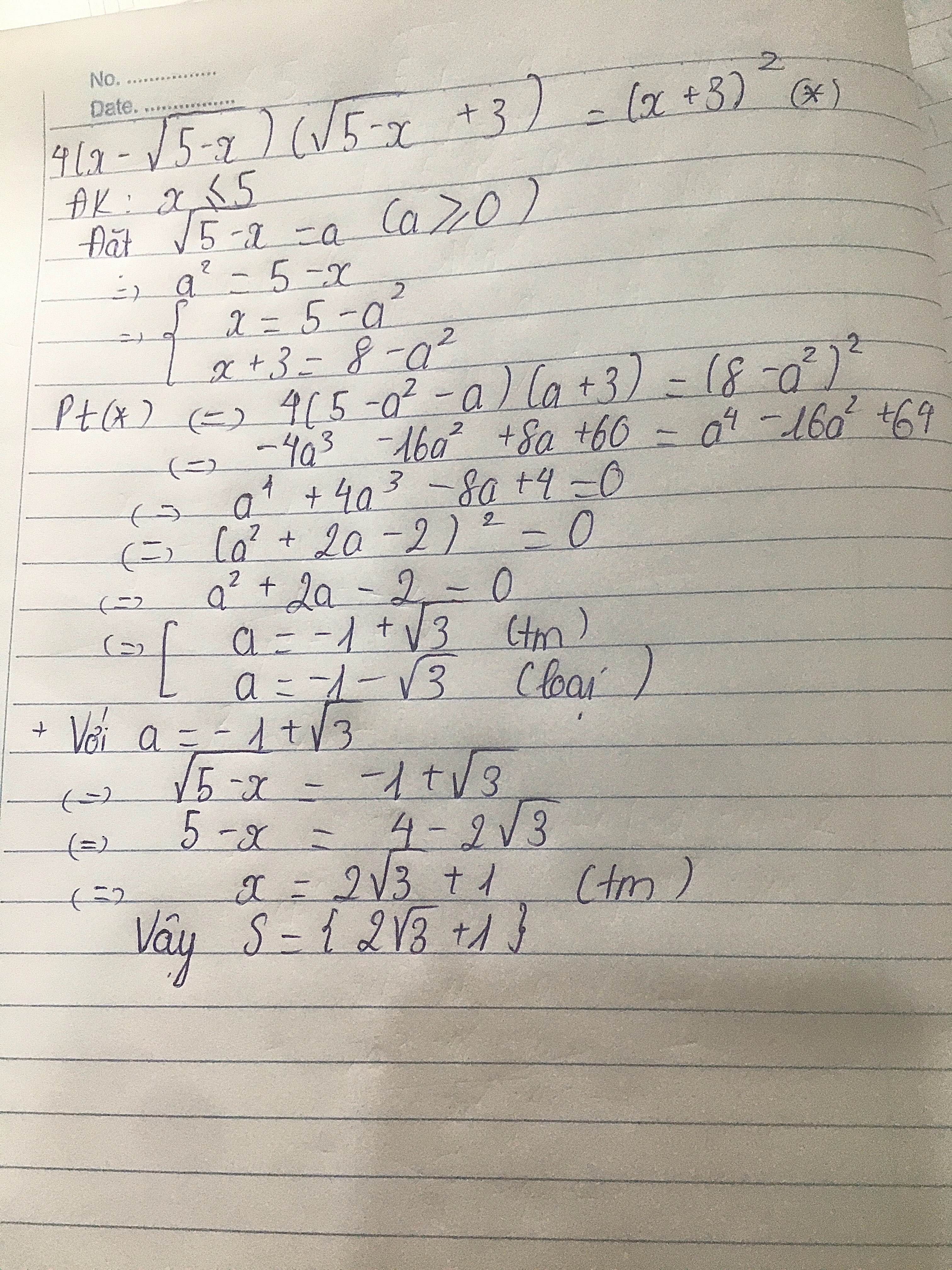
\(\left(x-7\right)\left(x-2\right)=x^2-9x+14\)
\(\left(x-5\right)\left(x-4\right)=x^2-9x+20\)
Đặt x^2-9x+14=y
\(y\left(y+6\right)=72\Leftrightarrow y^2+6y-72=0\)
\(\Delta'_y=3^2+72=81\)
\(\left\{\begin{matrix}y_1=-3+9=6\\y_2=-3-9=-12\end{matrix}\right.\)
\(x^2-9x+26=>\left(vonghiem\right)\)
\(x^2-9x+8=0\)
(a+b+c=0)
x1=1
x2=8
Kết luận:
pt đã chó có hai N0 x1=1 và x2=8
pt đã chó