Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\dfrac{x-2}{2000}+\dfrac{x-3}{1999}=\dfrac{x-4}{1998}+\dfrac{x-5}{1997}\\ \Leftrightarrow\dfrac{x-2}{2000}-1+\dfrac{x-3}{1999}-1=\dfrac{x-4}{1998}-1+\dfrac{x-5}{1997}-1\\ \Leftrightarrow\dfrac{x-2}{2000}-\dfrac{2000}{2000}+\dfrac{x-3}{1999}-\dfrac{1999}{1999}=\dfrac{x-4}{1998}-\dfrac{1998}{1998}+\dfrac{x-5}{1997}-\dfrac{1997}{1997}\\ \Leftrightarrow\dfrac{x-2002}{2000}+\dfrac{x-2002}{1999}=\dfrac{x-2002}{1998}+\dfrac{x-2002}{1997}\\ \Leftrightarrow\dfrac{x-2002}{2000}+\dfrac{x-2002}{1999}-\dfrac{x-2002}{1998}-\dfrac{x-2002}{1997}=0\\ \Leftrightarrow\left(x-2002\right)\left(\dfrac{1}{2000}+\dfrac{1}{1999}-\dfrac{1}{1998}-\dfrac{1}{1997}\right)=0\\ \)
\(Do:\dfrac{1}{2000}+\dfrac{1}{1999}-\dfrac{1}{1998}-\dfrac{1}{1997}\ne0\\ \Rightarrow x-2002=0\\ \Leftrightarrow x=2002\\ Vậy:S=\left\{2002\right\}\)
Mấy câu khác tương tự :v
b: \(\Leftrightarrow\left(\dfrac{148-x}{25}-1\right)+\left(\dfrac{169-x}{23}-2\right)+\left(\dfrac{186-x}{21}-3\right)+\left(\dfrac{199-x}{19}-4\right)=0\)
=>123-x=0
=>x=123
c: \(\Leftrightarrow\dfrac{x-2}{2017}+1=\dfrac{x-1}{2018}+\dfrac{x}{2019}\)
\(\Leftrightarrow\left(\dfrac{x-2}{2017}-1\right)=\left(\dfrac{x-1}{2018}-1\right)+\left(\dfrac{x}{2019}-1\right)\)
=>x-2019=0
=>x=2019

a: Ta có: \(4x-2\left(1-x\right)=5\left(x-4\right)\)
\(\Leftrightarrow4x-2+2x=5x-20\)
\(\Leftrightarrow x=-18\)
b: Ta có: \(\dfrac{x}{6}+\dfrac{1-3x}{9}=\dfrac{-x+1}{12}\)
\(\Leftrightarrow6x+4\left(1-3x\right)=3\left(-x+1\right)\)
\(\Leftrightarrow6x+4-12x=-3x+3\)
\(\Leftrightarrow-3x=-1\)
hay \(x=\dfrac{1}{3}\)
c: Ta có: \(\left(x+2\right)^2-3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

148-x/25-1 + 169-x/23-2 + 186-x/21-3 + 199-x/19-4
123-x/25 + 123-x/23 + 123-x/21 + 123-x/19 =0
123-x=0 => x=123
\(\frac{148-x}{25}+\frac{169-x}{23}+\frac{186-x}{21}+\frac{199-x}{19}=10\)
\(\left(\frac{148-x}{25}-1\right)+\left(\frac{169-x}{23}-2\right)+\left(\frac{186-x}{21}-3\right)+\left(\frac{199-x}{19}-4\right)=0\)
=> \(\frac{123-x}{25}+\frac{123-x}{23}+\frac{123-x}{21}+\frac{123-x}{19}=0\)
=> \(\left(123-x\right)\left(\frac{1}{25}+\frac{1}{23}+\frac{1}{21}+\frac{1}{19}\right)=0\)
=> 123 - x = 0
=> x = 123

a) ĐKXĐ: \(x\ne3\)
Ta có: \(\dfrac{x^2-x-6}{x-3}=0\)
\(\Leftrightarrow\dfrac{\left(x+2\right)\left(x-3\right)}{x-3}=0\)
Suy ra: x+2=0
hay x=-2(thỏa ĐK)
Vậy: S={-2}
d)
ĐKXĐ: \(x\notin\left\{1;3\right\}\)
Ta có: \(\dfrac{x+5}{x-1}=\dfrac{x+1}{x-3}-\dfrac{8}{x^2-4x+3}\)
\(\Leftrightarrow\dfrac{\left(x+5\right)\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}=\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-3\right)\left(x-1\right)}-\dfrac{8}{\left(x-1\right)\left(x-3\right)}\)
Suy ra: \(x^2-3x+5x-15=x^2-1-8\)
\(\Leftrightarrow2x-15+9=0\)
\(\Leftrightarrow2x-6=0\)
hay x=3(loại)
Vậy: \(S=\varnothing\)

1)
\(\dfrac{x-5}{100}+\dfrac{x-4}{101}+\dfrac{x-3}{102}=\dfrac{x-100}{5}+\dfrac{x-101}{4}+\dfrac{x-102}{3}\)
\(\Leftrightarrow\dfrac{x-5}{100}+1+\dfrac{x-4}{101}+1+\dfrac{x-3}{102}+1=\dfrac{x-100}{5}+1+\dfrac{x-101}{4}+1+\dfrac{x-102}{3}+1\)
\(\Leftrightarrow\dfrac{x-105}{100}+\dfrac{x-105}{101}+\dfrac{x-105}{102}=\dfrac{x-105}{5}+\dfrac{x-105}{4}+\dfrac{x-105}{3}+\dfrac{x-105}{2}\)
\(\Leftrightarrow\dfrac{x-105}{100}+\dfrac{x-105}{101}+\dfrac{x-105}{102}-\dfrac{x-105}{5}-\dfrac{x-105}{4}-\dfrac{x-105}{3}-\dfrac{x-105}{2}=0\)
\(\Leftrightarrow\left(x-105\right)\left(\dfrac{1}{100}+\dfrac{1}{101}+\dfrac{1}{102}-\dfrac{1}{5}-\dfrac{1}{4}-\dfrac{1}{3}-\dfrac{1}{2}\right)=0\)\(\Leftrightarrow105-x=0\)
\(\Leftrightarrow x=105\)
b)
\(\dfrac{29-x}{21}+\dfrac{27-x}{23}+\dfrac{25-x}{25}+\dfrac{23-x}{27}+\dfrac{21-x}{29}=0\)
\(\Leftrightarrow\dfrac{29-x}{21}+1+\dfrac{27-x}{23}+1+\dfrac{25-x}{25}+1+\dfrac{23-x}{27}+1+\dfrac{21-x}{29}+1=0\)
\(\Leftrightarrow\dfrac{50-x}{21}+\dfrac{50-x}{23}+\dfrac{50-x}{25}+\dfrac{20-x}{27}+\dfrac{50-x}{29}=0\)
\(\Leftrightarrow\left(50-x\right)\left(\dfrac{1}{21}+\dfrac{1}{23}+\dfrac{1}{25}+\dfrac{1}{27}+\dfrac{1}{29}\right)=0\)
\(\Leftrightarrow50-x=0\)
\(\Leftrightarrow x=50\)
2)
\(\left(5x+1\right)^2=\left(3x-2\right)^2\)
\(\Leftrightarrow\left|5x+1\right|=\left|3x-2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+1=3x-2\\5x+1=-3x+2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{2}\\x=\dfrac{1}{8}\end{matrix}\right.\)
b) \(\left(x+2\right)^3=\left(2x+1\right)^3\)
\(\Leftrightarrow x^3+6x^2+12x+8=8x^3+12x^2+6x+1\)
\(\Leftrightarrow-7x^3-6x^2+6x+7=0\)
\(\Leftrightarrow-7x^3+7x^2-13x^2+13x-7x+7=0\)
\(\Leftrightarrow-7x^2\left(x-1\right)-13x\left(x-1\right)-7\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-7x^2-13x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-7x^2-13x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\-7\left(x^2+\dfrac{13}{7}x+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\-7\left(x+\dfrac{13}{14}\right)^2-\dfrac{169}{196}=0\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=1\)

TK
https://lazi.vn/edu/exercise/giai-phuong-trinh-4x-5-x-1-2-x-x-1-7-x-2-3-x-5
a: \(\Leftrightarrow4x-5=2x-2+x\)
=>4x-5=3x-2
=>x=3(nhận)
b: =>7x-35=3x+6
=>4x=41
hay x=41/4(nhận)
c: \(\Leftrightarrow\dfrac{14}{3\left(x-4\right)}-\dfrac{x+2}{x-4}=\dfrac{-3}{2\left(x-4\right)}-\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{28}{6\left(x-4\right)}-\dfrac{6\left(x+2\right)}{6\left(x-4\right)}=\dfrac{-9}{6\left(x-4\right)}-\dfrac{5\left(x-4\right)}{6\left(x-4\right)}\)
\(\Leftrightarrow28-6x-12=-9-5x+20\)
=>-6x+16=-5x+11
=>-x=-5
hay x=5(nhận)
d: \(\Leftrightarrow x^2+2x+1-\left(x^2-2x+1\right)=16\)
\(\Leftrightarrow4x=16\)
hay x=4(nhận)

Bải 3a
\(\dfrac{-a+b+c}{2a}+\dfrac{-b+c+a}{2b}+\dfrac{-c+a+b}{2c}\ge\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{-a}{2a}+\dfrac{b+c}{2a}+\dfrac{-b}{2b}+\dfrac{c+a}{2b}+\dfrac{-c}{2c}+\dfrac{a+b}{2c}\ge\dfrac{3}{2}\)
\(\Leftrightarrow-\dfrac{3}{2}+\dfrac{b+c}{2a}+\dfrac{c+a}{2b}+\dfrac{a+b}{2c}\ge\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{b+c}{2a}+\dfrac{c+a}{2b}+\dfrac{a+b}{2c}\ge3\)
\(\Leftrightarrow\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\ge6\)
\(\Leftrightarrow\left(\dfrac{a}{b}+\dfrac{b}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{c}{a}+\dfrac{a}{c}\right)\ge6\)
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ba}}=2\\\dfrac{b}{c}+\dfrac{c}{b}\ge2\sqrt{\dfrac{bc}{cb}}=2\\\dfrac{c}{a}+\dfrac{a}{c}\ge2\sqrt{\dfrac{ca}{ac}}=2\end{matrix}\right.\)
\(\Rightarrow\left(\dfrac{a}{b}+\dfrac{b}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{c}{a}+\dfrac{a}{c}\right)\ge2+2+2=6\)
\(\Leftrightarrow\dfrac{-a+b+c}{2a}+\dfrac{-b+c+a}{2b}+\dfrac{-c+a+b}{2c}\ge\dfrac{3}{2}\) ( đpcm )
Dấu " = " xảy ra khi \(a=b=c\)
Bài 3b)
\(P=\dfrac{x}{y+z}+\dfrac{y}{x+z}+\dfrac{z}{x+y}\)
\(P=\dfrac{x^2}{xy+xz}+\dfrac{y^2}{xy+yz}+\dfrac{z^2}{xz+yz}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dạng phân thức
\(\Rightarrow\dfrac{x^2}{xy+xz}+\dfrac{y^2}{xy+yz}+\dfrac{z^2}{xz+yz}\ge\dfrac{\left(x+y+z\right)^2}{2\left(xy+yz+xz\right)}\)( 1 )
Theo hệ quả của bất đẳng thức Cauchy
\(\Rightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+xz\right)\)
\(\Rightarrow\dfrac{\left(x+y+z\right)^2}{2\left(xy+yz+xz\right)}\ge\dfrac{3\left(xy+yz+xz\right)}{2\left(xy+yz+xz\right)}=\dfrac{3}{2}\) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow\)\(\dfrac{x^2}{xy+xz}+\dfrac{y^2}{xy+yz}+\dfrac{z^2}{xz+yz}\ge\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{x}{y+z}+\dfrac{y}{x+z}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\)
\(\Leftrightarrow P\ge\dfrac{3}{2}\)
Vậy \(P_{min}=\dfrac{3}{2}\)
Dấu " = " xảy ra khi \(a=b=c\)
Bài 2:
a) \(\dfrac{x-17}{33}+\dfrac{x-21}{29}+\dfrac{x}{25}=4\)
\(\Rightarrow\left(\dfrac{x-17}{33}-1\right)+\left(\dfrac{x-21}{29}-1\right)+\left(\dfrac{x}{25}-2\right)=0\)
\(\Rightarrow\dfrac{x-50}{33}+\dfrac{x-50}{29}+\dfrac{x-50}{25}=0\)
\(\Rightarrow\left(x-50\right)\left(\dfrac{1}{33}+\dfrac{1}{29}+\dfrac{1}{25}\right)=0\)
Mà \(\dfrac{1}{33}+\dfrac{1}{29}+\dfrac{1}{25}\ne0\)
\(\Rightarrow x-50=0\)
\(\Rightarrow x=50\)
Vậy x = 50

a: Ta có: \(3x-\left(3x+2\right)=x+3\)
\(\Leftrightarrow x+3=-2\)
hay x=-5
b: Ta có: \(\dfrac{5x-1}{4}+\dfrac{2x-1}{3}=\dfrac{3x}{2}\)
\(\Leftrightarrow15x-3+8x-4=18x\)
\(\Leftrightarrow5x=7\)
hay \(x=\dfrac{7}{5}\)

a: =>3,6-1,7x=2,3-1,4-4=0,9-4=-3,1
=>1,7x=6,7
hay x=67/17
b: \(\Leftrightarrow30\left(5x+4\right)-15\left(3x+5\right)=24\left(4x+9\right)-40\left(x-9\right)\)
=>150x+120-45x-75=96x+216-40x+360
=>105x+45=56x+576
=>49x=531
hay x=531/49
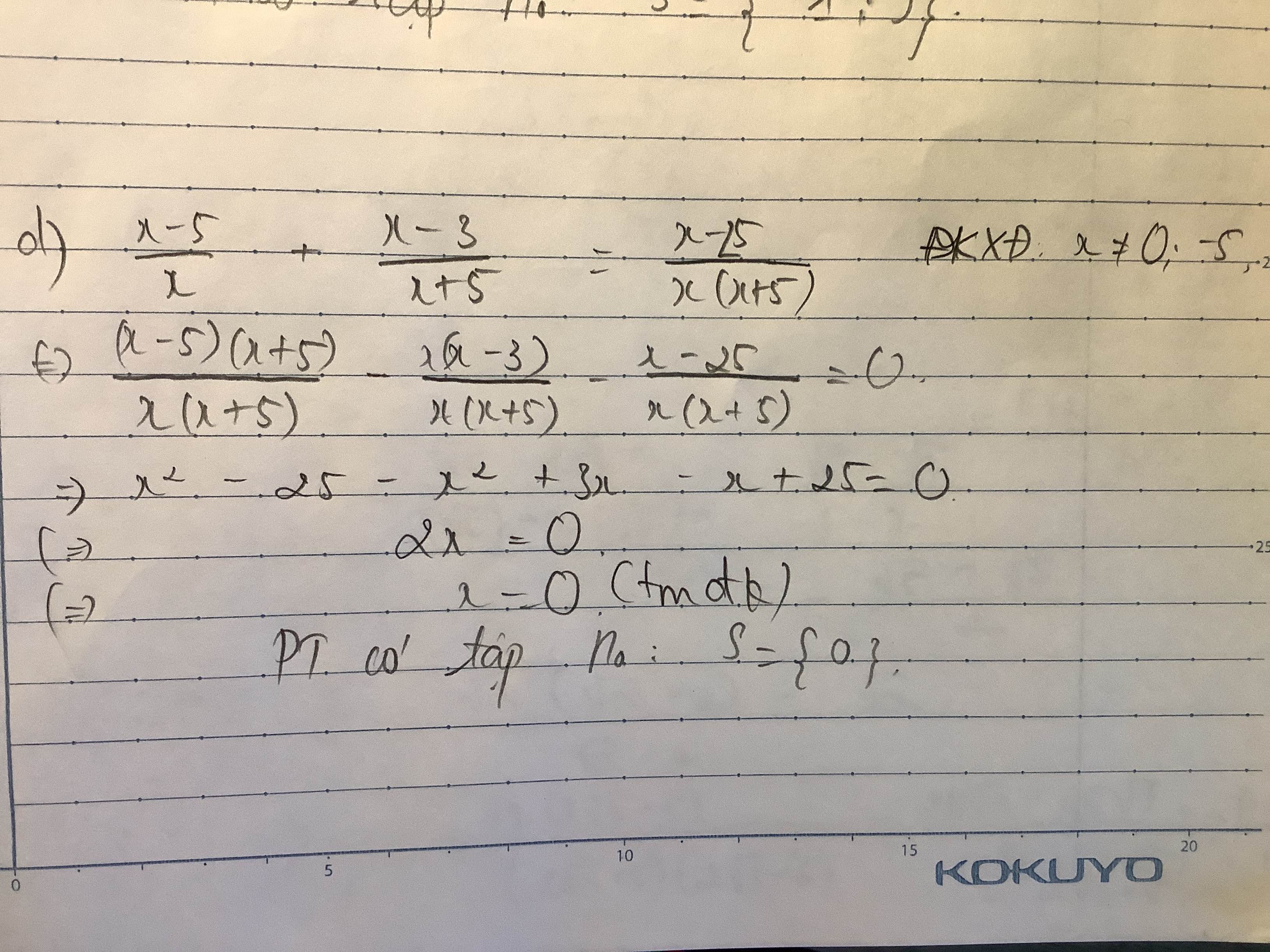
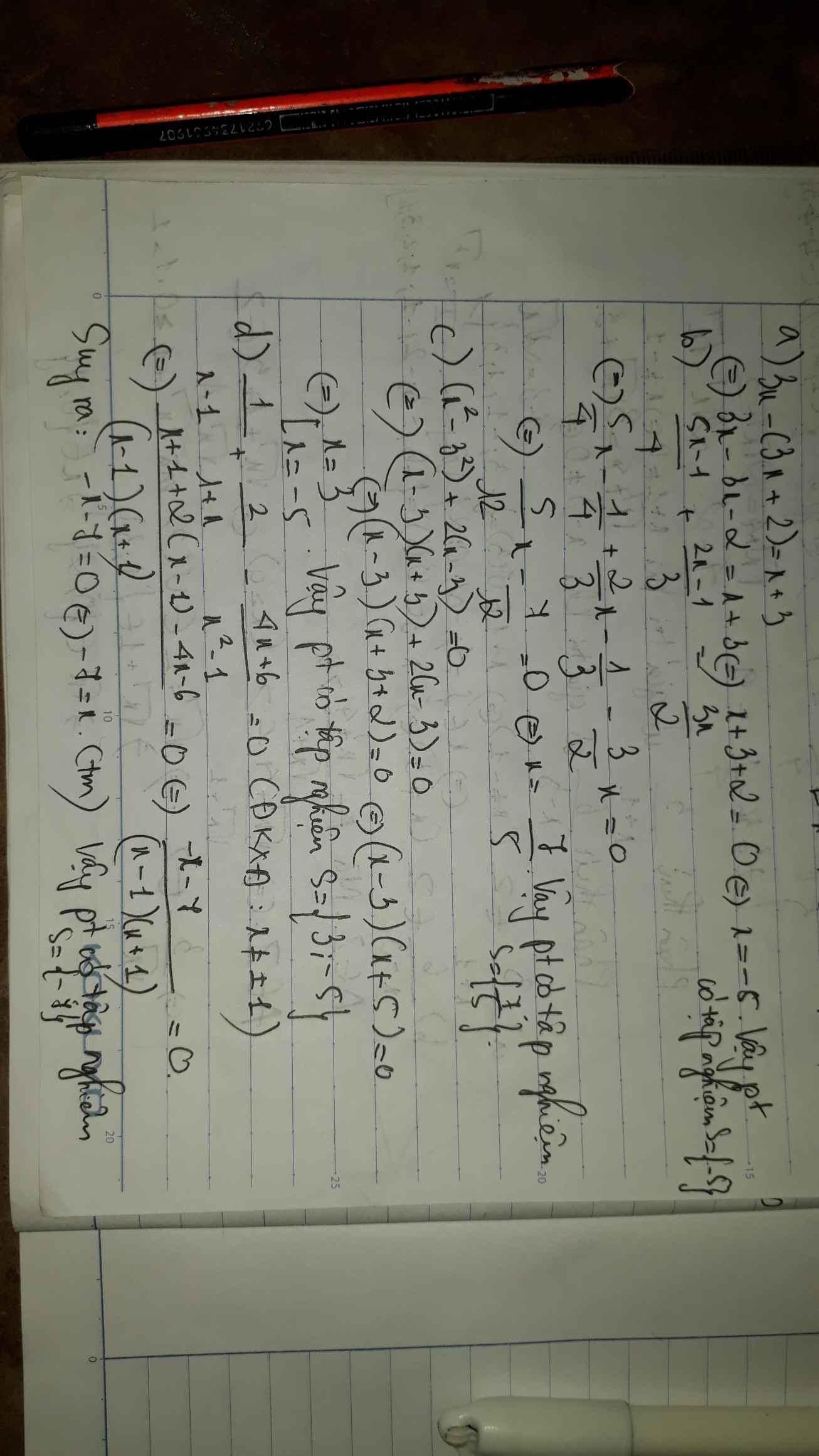
c: =>|x-2|+3=-5 hoặc |x-2|+3=5
=>|x-2|=2
=>x-2=2 hoặc x-2=-2
=>x=4 hoặc x=0