K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
27 tháng 1 2017
Đặt m = t 2 .Điều kiện m ≥ 0
Ta có: 36 t 4 – 13 t 2 +1 = 0 ⇔ 36 m 2 -13m +1 =0
Ta có: ∆ = - 13 2 – 4.36.1=169 -144=25 > 0
∆ = 25 = 5
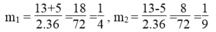
Ta có: t 2 =1/4 ⇒ t= ± 1/2
t 2 =1/9 ⇒ t= ± 1/3
Vậy phương trình đã cho có 4 nghiệm :
t 1 = 1/2 ; t 2 = -1/2 ; t 3 = 1/3 ; t 4 = -1/3
TN
24 tháng 5 2017
\(x^4+5x^2-36=0\)
\(\Leftrightarrow x^4-4x^2+9x^2-36=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+9\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x^2+9\right)=0\)
Dễ thấy: \(x^2+9\ge9>0\forall x\) (vô nghiệm)
SUy ra \(x-2=0;x+2=0\Rightarrow x=2;x=-2\)
SY
24 tháng 5 2017
Đặt t = x2 ( t ≥ 0)
ta có phương trình: t2 + 5t – 36 = 0. Δt = 25 4.1.(-36) = 169
→ t1 = 4 (tmđk); t2 = -9 (loại). Với t = 4 → x2 = 4 → x = 2
AH
Akai Haruma
Giáo viên
29 tháng 5 2023
Lời giải:
Lấy P(1) + 4PT(2) ta được:
$\sqrt{2x-y-9}+x^2-4xy+4y^2=0$
$\Leftrightarrow \sqrt{2x-y-9}+(2y-x)^2=0$
Do $\sqrt{2x-y-9}\geq 0; (2y-x)^2\geq 0$ với mọi $x,y$ tm điều kiện xác định nên để tổng của chúng bằng 0 thì:
$2x-y-9=2y-x=0$
$\Leftrightarrow 2x-y=9; x=2y$
$\Rightarrow x=18; y=9$
LT
1
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 9 2017
ĐK: \(\hept{\begin{cases}x-5\ge0\\x-4-2\sqrt{x-5}\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge5\\\left(\sqrt{x-5}-1\right)^2\ge0\end{cases}}\Leftrightarrow x\ge5\)
\(\sqrt{36\left(x-4-2\sqrt{x-5}\right)}-18=0\)
\(\Leftrightarrow\sqrt{36\left(x-4-2\sqrt{x-5}\right)}=18\)
\(\Leftrightarrow\left(x-4-2\sqrt{x-5}\right)=9\)
\(\Leftrightarrow\left(\sqrt{x-5}-1\right)^2=9\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-5}-1=3\\\sqrt{x-5}-1=-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}\sqrt{x-5}=4\left(tm\right)\\\sqrt{x-5}=-2\left(l\right)\end{cases}}\Leftrightarrow x=21\left(tm\right)\)
NM
7
12 tháng 6 2016
a, x4 - 13x2 + 36 = 0
Đặt : x2 = t , t > 0 , ta có :
t2 - 13t + 36 = 0 \(\Leftrightarrow\) t = 9 hay t = 4
- Với t = 9 \(\Rightarrow\) x2 = 9 \(\Rightarrow\) x = + 3
- Với t = 4 \(\Rightarrow\) x2 = 4 \(\Rightarrow\) x = + 2
Vậy phương trình có 4 nghiệm
x1 = 3 ; x2 = -3 ; x3 = 2 ; x4 = -2
b, 3x4 + 7x2 - 10 =0
Đặt : x2 = t , t > 0 , ta có :
3t2 + 7t - 10 = 0
\(\Leftrightarrow\) t = 1 hay t = -\(\frac{10}{3}\) (loại )
- Với t = 1 \(\Rightarrow\) x2 = 1 \(\Rightarrow\) x = +1
Phương trình có hai nghiệm là :
x1 = 1 ; x2 = -1
7 tháng 9 2021
a) \(x^4-13x^2+36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\\x=-3\end{matrix}\right.\)
b) \(5x^4+3x^2-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(5x^2+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)( do \(5x^2+8\ge8>0\))
7 tháng 9 2021
c: Ta có: \(2x^4+3x^2+2=0\)
Đặt \(a=x^2\)
Phương trình tương đương là: \(2a^2+3a+2=0\)
\(\text{Δ}=3^2-4\cdot2\cdot2=9-16=-7\)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Phương trình \(2x^4+3x^2+2=0\) vô nghiệm
LK
2
4 tháng 12 2021
\(\Leftrightarrow\left|2x+1\right|=\left|x+6\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=x+6\\2x+1=-x-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{7}{3}\end{matrix}\right.\)
TK
1
13 tháng 10 2021
\(9x^2+2\sqrt{x^2-4}=36\left(x\le-2;x\ge2\right)\\ \Leftrightarrow2\sqrt{x^2-4}+9x^2-36=0\\ \Leftrightarrow2\sqrt{x^2-4}+9\left(x^2-4\right)=0\\ \Leftrightarrow\sqrt{x^2-4}\left(2+9\sqrt{x^2-4}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-4=0\\\sqrt{x^2-4}=-\dfrac{2}{9}\left(vô.nghiệm\right)\end{matrix}\right.\\ \Leftrightarrow x^2-4=0\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)
CM
7 tháng 1 2018
x2 – x – 2 = 0
Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.
Vậy tập nghiệm của phương trình là S = {-1; 2}
Đặt \(x^2=u\left(u\ge0\right)\), pt đã cho trở thành \(-36u^2+97u-36=0\) (*)
pt (*) có \(\Delta=97^2-4\left(-36\right)\left(-36\right)=4225>0\)
Nên pt này có 2 nghiệm phân biệt \(\left[{}\begin{matrix}u_1=\dfrac{-97+\sqrt{4225}}{2.\left(-36\right)}=\dfrac{4}{9}\left(nhận\right)\\u_2=\dfrac{-97-\sqrt{4225}}{2\left(-36\right)}=\dfrac{9}{4}\left(nhận\right)\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2=\dfrac{4}{9}\\x^2=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{2}{3}\\x=\pm\dfrac{3}{2}\end{matrix}\right.\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm\dfrac{2}{3};\pm\dfrac{3}{2}\right\}\)