TT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DS
0
PT
1
CM
14 tháng 2 2019
Chọn C
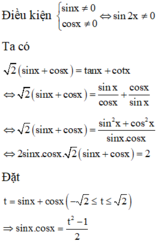
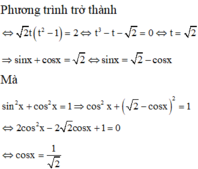
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đầu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:
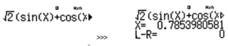
Tiếp theo ta tính cos x thì dễ thấy được:
Đến đây ta dễ dàng chọn được phương án C là phương án đúng thay cho lời giải tự luận nhiều phức tạp.
HP
31 tháng 5 2021
1.
ĐK: \(x\ne\dfrac{k\pi}{2}\)
\(cotx-tanx=sinx+cosx\)
\(\Leftrightarrow\dfrac{cosx}{sinx}-\dfrac{sinx}{cosx}=sinx+cosx\)
\(\Leftrightarrow\dfrac{cos^2x-sin^2x}{sinx.cosx}=sinx+cosx\)
\(\Leftrightarrow\left(\dfrac{cosx-sinx}{sinx.cosx}-1\right)\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(1\right)\\cosx-sinx=sinx.cosx\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\)
\(\left(2\right)\Leftrightarrow t=\dfrac{1-t^2}{2}\left(t=cosx-sinx,\left|t\right|\le2\right)\)
\(\Leftrightarrow t^2+2t-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow cosx-sinx=-1+\sqrt{2}\)
\(\Leftrightarrow-\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=-1+\sqrt{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\\x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=-\dfrac{\pi}{4}+k\pi;x=\dfrac{\pi}{4}+arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi;x=\dfrac{5\pi}{4}-arcsin\left(\dfrac{\sqrt{2}-1}{\sqrt{2}}\right)+k2\pi\)
![Giải phương trình lượng giác,1 + tanx = 2căn2.sinx,[sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2),Toán học Lớp 11,bài tập Toán học Lớp 11,giải bài tập Toán học Lớp 11,Toán học,Lớp 11](https://lazi.vn/uploads/edu/answer/1502109525_502.jpg "Giải phương trình lượng giác: a) 1 + tanx = 2√2.sinx; b) [sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2) - Toán học Lớp 11 - Bài tập Toán học Lớp 11 - Giải bài tập Toán học Lớp 11")
![Giải phương trình lượng giác,1 + tanx = 2căn2.sinx,[sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2),Toán học Lớp 11,bài tập Toán học Lớp 11,giải bài tập Toán học Lớp 11,Toán học,Lớp 11](https://lazi.vn/uploads/edu/answer/1502117801_501.jpg "Giải phương trình lượng giác: a) 1 + tanx = 2√2.sinx; b) [sin^2x(sinx - 1)] : (sinx + cosx) = 4cos^2(x/2) - Toán học Lớp 11 - Bài tập Toán học Lớp 11 - Giải bài tập Toán học Lớp 11")
N
11 tháng 9 2016
a)pt\(\Leftrightarrow cosx\left(cosx+1\right)+sinx.sin^2x=0\)
\(\Leftrightarrow cosx\left(cosx+1\right)+sinx\left(1-cos^2x\right)=0\)
\(\Leftrightarrow\left(cosx+1\right)\left(cosx+sinx-sinx.cosx\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}cosx=1\Leftrightarrow x=\pi+k2\pi\\cosx+sinx-sinx.cosx=0\left(\cdot\right)\end{array}\right.\)
Xét pt(*):
Đặt \(t=cosx+sinx,t\in\left[-\sqrt{2};\sqrt{2}\right]\Rightarrow sinx.cosx=\frac{t^2-1}{2}\)
(*) trở thành:\(t^2-2t-1=0\Leftrightarrow\left[\begin{array}{nghiempt}t=1-\sqrt{2}\\t=1+\sqrt{2}\left(L\right)\end{array}\right.\)
+)\(t=1-\sqrt{2}\Rightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1-\sqrt{2}\\ \Leftrightarrow\left[\begin{array}{nghiempt}x=-\frac{\pi}{4}+arcsin\left(\frac{-2+\sqrt{2}}{2}\right)+k2\pi\\x=-\frac{5\pi}{4}-arcsin\left(\frac{-2+\sqrt{2}}{2}\right)+k2\pi\end{cases}\left(k\in Z\right)}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
ĐK: \(cosx\ne0\Leftrightarrow x\ne\frac{\pi}{2}+k\pi,k\inℤ\).
\(1+tanx=2\left(sinx+cosx\right)\)
\(\Leftrightarrow cosx+sinx=2cosx\left(sinx+cosx\right)\)
\(\Leftrightarrow\orbr{\begin{cases}sinx+cosx=0\\cosx=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=cos\left(-x-\frac{\pi}{2}\right)\\cosx=cos\frac{\pi}{3}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\pm\left(-x-\frac{\pi}{2}\right)+k2\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{cases}},\left(k\inℤ\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{-\pi}{4}+k\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{cases}},\left(k\inℤ\right)\)(thỏa mãn)
\(1+\tan x=2\left(\sin x+\cos x\right)\)
Bạn áp dụng đẳng thức lượng giác nhé :
\(\frac{\sin x+\cos x}{\cos x}=2\sin x+2\cos x\)
Biệt thức :
\(D=b^2-4ac\)
\(\Leftrightarrow\left(-1\right)^2-4\left(1.1\right)=-3\)
Phương trình không có nghiệm thực :
\(D< 0\)
Nghiệm tuần hoàn :
\(2\pi k-\frac{\pi}{4}\)
\(2\pi k+\frac{3\pi}{4}\)
\(2\pi k+\frac{\pi}{3}\)
\(2\pi k-\frac{\pi}{3}\)
Ps : không hiểu chỗ nào thì bạn hỏi mình nhé, nhớ k :33
# Aeri #