Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

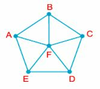
Tất cả các đỉnh A, B, C, D, E đều nối với đỉnh F nên đỉnh F phải tô màu khác với các đỉnh còn lại. Với 5 đỉnh còn lại thì A và C tô cùng một màu. B và D tô cùng một màu, E tô riêng một màu, như vậy cần ít nhất 3 màu để tô 5 đỉnh sao cho 2 đỉnh được nối bởi một cạnh được tô bởi 2 màu khác nhau. Vậy cần ít nhất 4 màu để tô 6 đỉnh của hình theo yêu cầu của đề bài.

Diện tích một mặt của hình lập phương lớn là: 600 : 6 = 100 (cm2)
Ta thấy: 100 = 10 x 10, do đó cạnh của hình lập phương lớn là 10cm.
Công thức tính số hình lập phương nhỏ được sơn 2 mặt là: 3xa'x4, trong đó a' bằng độ dài cạnh của hình lập phương lớn trừ đi 2.
Số hình lập phương nhỏ được sơn 2 mặt là: 3x(10-2)x4 = 96 (hình) (trong trường hợp không bỏ đi hình lập phương nhỏ nào)
Nếu bỏ một hình lập phương nhỏ ở một đỉnh thì lúc này số hình lập phương nhỏ được sơn 2 mặt giảm đi 3 hình.
Do người ta bỏ đi 4 hình lập phương nhỏ ở bốn đỉnh nên số hình lập phương nhỏ được sơn 2 mặt lúc này là:
96 - 3x4 = 84 (hình)
Đáp số: 84 hình
Diện tích một mặt của hình lập phương lớn là 600 : 6 = 100cm2
Suy ra cạnh của hình lập phương lớn là 10cm tương đương với 10 hình lập phương nhỏ.
Số lượng hình lập phương nhỏ của một mặt được sơn cả hai mặt là 10 x 4 - 4 = 36 (hình)
Số lượng hình lập phương nhỏ của hai mặt đối diện (song song) được sơn cả hai mặt là 36 x 2 = 72 (hình)
Số lượng hình lập phương nhỏ còn lại được sơn cả hai mặt là (10 - 2) x 2 - 4 = 12 (hình)
Tổng số hình lập phương nhỏ được sơn cả hai mặt là 72 + 12 = 84 (hình)

chịu , khó hiểu quá linh ơi
Bạn giải toán quốc tế bricmaths hả
Mình làm được bài đấy rồi
cần thiết thì mình chụp cho