giải hộ mình vs ạ mình cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VQ
0
14 tháng 6 2023
a: góc ASB=1/2*180=90 độ=góc ABM
b: ON vuông góc AS
BS vuông góc SA
=>ON//BS
c: góc OIM+góc OBM=180 độ
=>OIMB nội tiếp
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
KA
1
21 tháng 10 2021
Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
29 tháng 6 2021
`a)sqrtx=sqrt{16+6sqrt7}`
`=sqrt{9+2.3sqrt7+7}`
`=sqrt{(3+sqrt7)^2}`
`=3+sqrt7`
`b)sqrtx=sqrt{4-2sqrt3}=sqrt{3-2sqrt3+1}=sqrt{(sqrt3-1)^2}=sqrt3-1`
`c)sqrtx=sqrt{13+4sqrt3}=sqrt{12+2.2sqrt3+1}=sqrt{(2sqrt3+1)^2}=2sqrt3+1`
29 tháng 6 2021
a) \(x=16+6\sqrt{7}\)
\(\Rightarrow\sqrt{x}=\sqrt{16+6\sqrt{7}}\)
\(\Rightarrow\sqrt{x}=\sqrt{7+6\sqrt{7}+9}\)
\(\Rightarrow\sqrt{x}=\sqrt{7+6\sqrt{7}+3^2}\)
\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{7}+3\right)^2}\)
\(\Rightarrow\left(\sqrt{x}\right)^2=\sqrt{\left(\sqrt{7}+3\right)^2}\)
\(\Rightarrow\sqrt{7}+3\)
KL: x=\(\sqrt{7}+3\)
7 tháng 10 2021
a: \(x=\dfrac{6^2}{3}=12\left(cm\right)\)
\(y=\sqrt{6^2+12^2}=6\sqrt{5}\)
b: \(x=\sqrt{4\cdot9}=6\)
c: \(x=5\cdot\tan40^0\simeq4,2\left(cm\right)\)
23 tháng 12 2021
Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều
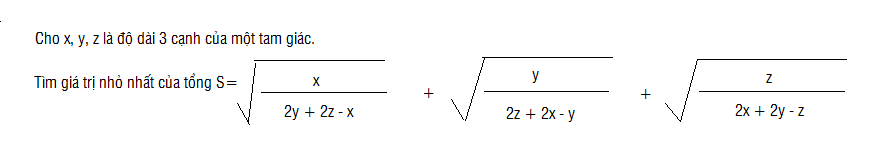
1)x>=0
2)v8+5v2-v32+6v1/2=2v2+5v2-4v2+3v2=9v2
3)vx+1=2
x+1=4=>x=3