
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4:
Ta có: \(A=x^2+4x+y^2-5y+20\)
\(=x^2+4x+4+y^2-5y+\dfrac{25}{4}+\dfrac{39}{4}\)
\(=\left(x+2\right)^2+\left(y-\dfrac{5}{2}\right)^2+\dfrac{39}{4}\ge\dfrac{39}{4}\forall x,y\)
Dấu '=' xảy ra khi x=-2 và \(y=\dfrac{5}{2}\)

Goi x,y,z lan luot la so luong xe loai 40 tan, 25 tan va 5 tan. Ta co:
2/3.x = 2/5.y = 3/7.z va: x+y+z = 114
=> x/(3/2) = y/(5/2) = z/(7/3) = (x+y+z)/(3/2+5/2+7/3) = 114/(19/3) = 18
=> x = 27 ; y = 45 ; z = 42
Vay: co 27 chiec xe loai 40 tan, 45 chiec loai 25 tan va 42 chiec loai 5 tan

a) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{360}{60}=6\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=6\\\dfrac{y}{4}=6\\\dfrac{z}{5}=6\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=24\\z=30\end{matrix}\right.\)
b) Áp dụng tính chất dãy tỉ số bằng nhau:\(\dfrac{x}{-2}=-\dfrac{y}{4}=\dfrac{z}{5}=-\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{-2+8+15}=\dfrac{1200}{21}=\dfrac{400}{7}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{-2}=\dfrac{400}{7}\\-\dfrac{y}{4}=\dfrac{400}{7}\\\dfrac{z}{5}=\dfrac{400}{7}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{800}{7}\\y=-\dfrac{1600}{7}\\z=\dfrac{2000}{7}\end{matrix}\right.\)
c) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{5}=\dfrac{y}{1}=\dfrac{z}{-2}=\dfrac{-2z}{4}=\dfrac{x+y-2z}{5+1+4}=\dfrac{160}{10}=16\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=16\\\dfrac{y}{1}=16\\\dfrac{z}{-2}=16\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=80\\y=16\\z=-32\end{matrix}\right.\)

\(x^2-4x+5=\left(x-2\right)^2+1\ge0\)
Vậy M(x) không có nghiệm
Vì \(x^2\ge0;4x\ge0\Rightarrow x^2-4x+5\ge0+5>0\)
\(\Rightarrow M\left(x\right)=x^2-4x+5\)không có nghiệm



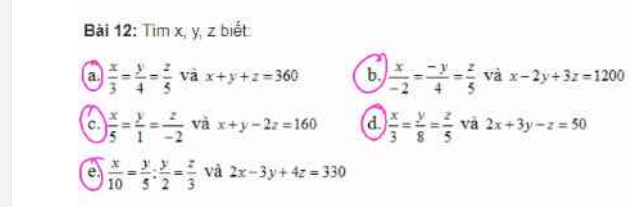 giải giúp mình bài này cảm ơn trước
giải giúp mình bài này cảm ơn trước
a) \(3\dfrac{1}{4}=\dfrac{2}{3}:\left(\dfrac{-x}{2}\right)\Leftrightarrow\dfrac{13}{4}=\dfrac{2}{3}.\dfrac{-2}{x}\Leftrightarrow\dfrac{-2}{x}=\dfrac{39}{8}\Leftrightarrow x=-\dfrac{16}{39}\)
b) \(1-2\left(x+\dfrac{1}{3}\right)=\left|-\dfrac{2}{3}+\dfrac{1}{5}\right|\Leftrightarrow1-2x-\dfrac{2}{3}=\dfrac{7}{15}\Leftrightarrow2x=-\dfrac{2}{15}\Leftrightarrow x=-\dfrac{1}{15}\)
c) \(\left(2x-1\right)\left(\dfrac{2}{5}-\dfrac{1}{3}x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\\dfrac{2}{5}-\dfrac{1}{3}x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\\dfrac{1}{3}x=\dfrac{2}{5}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{6}{5}\end{matrix}\right.\)
d) \(-4\dfrac{3}{5}.2\dfrac{4}{23}\le x\le-2\dfrac{3}{5}:1\dfrac{6}{15}\Leftrightarrow-10\le x\le-\dfrac{13}{7}\Leftrightarrow x\in\left\{-10;-9;-8;-7;-6;-5;-4;-3;-2;-1\right\}\)(do \(x\in Z\))
Bài 2:
c: Ta có: \(\left(2x-1\right)\left(\dfrac{2}{5}-\dfrac{1}{3}x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\\dfrac{2}{5}-\dfrac{1}{3}x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=1\\\dfrac{1}{3}x=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{6}{5}\end{matrix}\right.\)