
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: =>x+2022=0
hay x=-2022
b: \(\Leftrightarrow x-198=0\)
hay x=198


a: \(\left(3x-1\right)\left(2x+7\right)-\left(12x^3+8x^2-14x\right):2x\)
\(=6x^2+21x-2x-7-\left(6x^2+4x-7\right)\)
\(=6x^2+19x-7-6x^2-4x+7\)
=15x
b: \(B=\dfrac{63^3-37^3}{26}+63\cdot37\)
\(=63^2+63\cdot37+37^2+63\cdot37\)
=10000

\(a,\Leftrightarrow2x=-6\\ \Leftrightarrow x=-\dfrac{6}{2}=-3\)
\(Vậy.pt.có.tập.nghiệm.là.S=\left\{-3\right\}\)
\(b,\Leftrightarrow\) 2x - 4 = 0 hoặc \(\Leftrightarrow\) x + 3 = 0
\(\Leftrightarrow\) x = 2 \(\Leftrightarrow\) x = -3
Vậy phương trình có tập nghiệm S = \(\left\{2;-3\right\}\)
\(c,\Leftrightarrow x=\dfrac{7}{5}\)
Vậy phương trình có tập nghiệm S = \(\left\{\dfrac{7}{5}\right\}\)
\(d,\) \(\Leftrightarrow2x=0\) hoặc \(\Leftrightarrow\) \(x-3=0\)
\(\Leftrightarrow x=0\) \(\Leftrightarrow x=3\)
Vậy phương trình có tập nghiệm S = \(\left\{0;3\right\}\)
\(e,\Leftrightarrow5.\left(3x-3\right)+4.\left(2x-5\right)=80\)
\(\Leftrightarrow15x-15+8x-20=80\)
\(\Leftrightarrow15x+8x=80+15+20\\ \Leftrightarrow23x=115\\ \Leftrightarrow x=\dfrac{115}{23}=5\)
Vậy phương trình có tập nghiệm S = \(\left\{5\right\}\)
Bài này mình làm tắt 1 bước, bạn không hiểu thì nhắn tin hỏi mình nhé!
\(f,\Leftrightarrow2.\left(x+2\right)+3.\left(x-2\right)=5x-1\) ( Thêm ĐKXĐ: \(x\ne2;x\ne-2\) )
\(\Leftrightarrow2x+4+3x-6=5x-1\\ \Leftrightarrow2x+3x-5x=-1-4+6\Leftrightarrow0x=1\)
Vậy phương trình trên có tập nghiệm \(S=\varnothing\)

Câu 6 hôm qua mình làm cho bạn rồi nhé!
https://hoc24.vn/cau-hoi/giai-ho-mik-voi-can-gap-a.5422364311917
Câu 7:
Theo tính chất đường phân giác của tam giác, ta có:
=> \(\dfrac{BM}{AB}=\dfrac{MC}{AC}\)
Mà AB = 4 cm, AC = 6 cm, BC = 8 cm
Áp dụng t/c dãy tỉ số bằng nhau, ta lại có:
\(\dfrac{BM}{AB}=\dfrac{MC}{AC}=\dfrac{BM+MC}{AB+AC}=\dfrac{BC}{4+6}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\Rightarrow BM=\dfrac{4.4}{5}=3,2\left(cm\right)\)
\(\Rightarrow MC=\dfrac{6.4}{5}=4,8\left(cm\right)\)

vs đk tổng =1 ta có:
\(\dfrac{a+bc}{b+c}+\dfrac{b+ca}{c+a}+\dfrac{c+ab}{a+b}\)
\(=\dfrac{a\left(a+b+c\right)+bc}{bc}+\dfrac{b\left(a+b+c\right)+ca}{ca}+\dfrac{c\left(a+b+c\right)+ab}{ab}\)
\(=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\)
sd bđt AM-GM cho 2 số dương ta có:
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}\ge2\left(a+b\right)\)
\(\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(b+c\right)\)
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(c+a\right)\)
Cộng theo vế 3 đẳng thức trên ta sẽ có điều phải chứng minh
Đẳng thức xảy ra khi và chỉ khi a = b= c =\(\dfrac{1}{3}\)

Ta có: \(\Delta ABC\sim\Delta MNP\)
\(\Rightarrow\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}=\dfrac{1}{2}\)
mà AB = 4 cm, BC = 6 cm, AC = 5 cm. Thay vào, ta lại có:
\(\Rightarrow\dfrac{4}{MN}=\dfrac{5}{MP}=\dfrac{6}{NP}=\dfrac{1}{2}\)
\(\Rightarrow MN=\dfrac{2.4}{1}=8\left(cm\right)\)
\(\Rightarrow MP=5.2=10\left(cm\right)\)
\(\Rightarrow NP=6.2=12\left(cm\right)\)

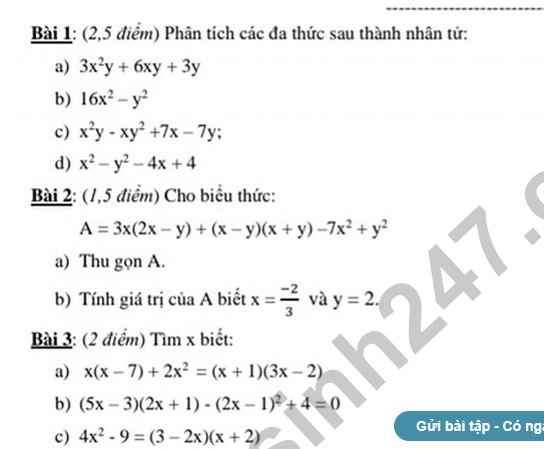

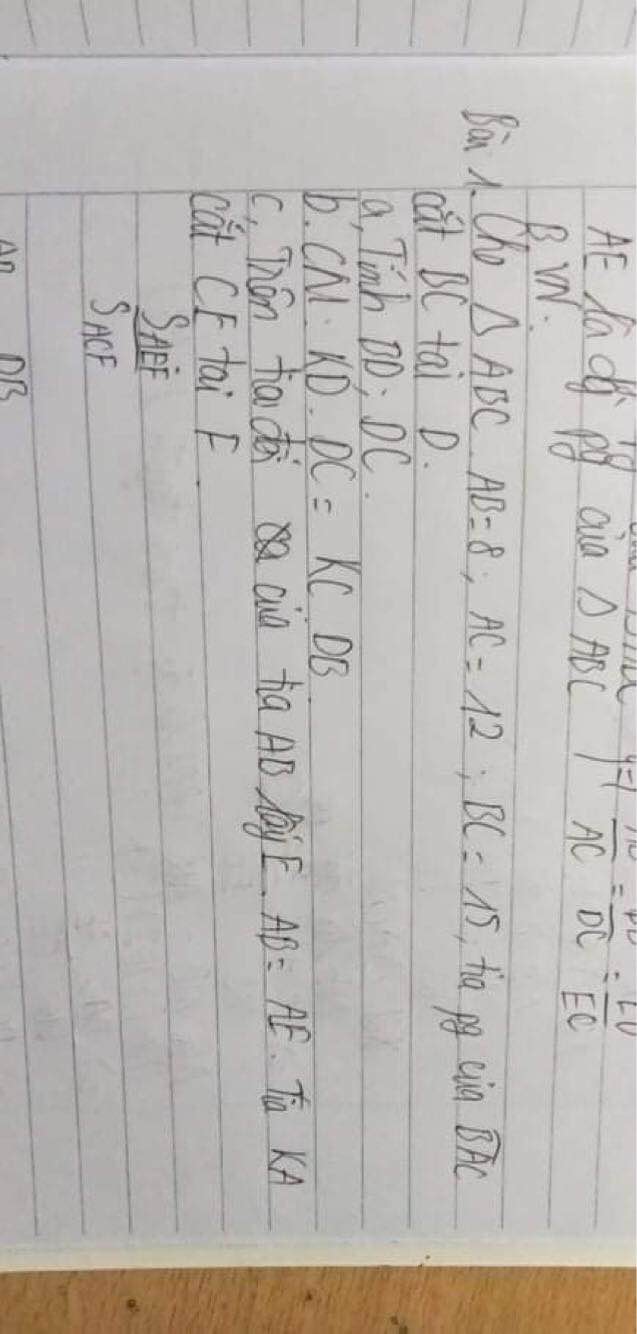
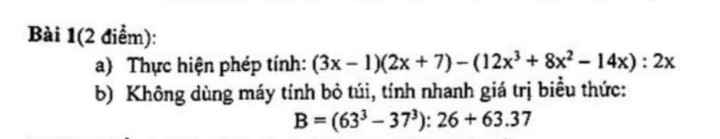




 giải chi tiết hộ mik với ạ.
giải chi tiết hộ mik với ạ.