KO
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
25 tháng 5 2016
bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
42.
ĐKXĐ: \(x>0\)
\(log_3^2x-5log_3x+6\le0\)
\(\Leftrightarrow\left(log_3x-2\right)\left(log_3x-3\right)\le0\)
\(\Rightarrow2\le log_3x\le3\)
\(\Rightarrow9\le x\le27\)
\(\Rightarrow2a-b=9.2-27=\)
43.
\(r=\dfrac{1}{2};h=1\)
\(\Rightarrow V=\pi r^2h=\dfrac{\pi}{4}\)
44.
ĐKXĐ: \(a>0\)
\(log_2a+log_23=log_2\left(2a+2\right)\)
\(\Leftrightarrow log_2\left(3a\right)=log_2\left(2a+2\right)\)
\(\Rightarrow3a=2a+2\)
\(\Rightarrow a=2\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
45.
\(V=\dfrac{1}{3}.6a.20a^2=40a^3\)
46.
Pt hoành độ giao điểm:
\(-x^2+2=x^3+2\Leftrightarrow x^3+x^2=0\)
\(\Leftrightarrow x^2\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
\(\Rightarrow\) Hai đồ thị có 2 giao điểm
47.
\(y'=x^2-5x+6=0\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(f\left(1\right)=\dfrac{29}{6}\) ; \(f\left(2\right)=\dfrac{17}{3}\) ; \(f\left(3\right)=\dfrac{11}{2}\)
\(\Rightarrow\) Hàm đạt min tại \(x=1\) và đạt max tại \(x=2\)
\(\Rightarrow x_1+x_2=3\)
48.
\(y'=-4x^3=0\Rightarrow x=0\)
Do \(a=-1< 0\Rightarrow\)hàm đồng biến trên \(\left(-\infty;0\right)\)
49.
\(y'=3ax^2+2bx+c\Rightarrow\left\{{}\begin{matrix}c=0\\12a+4b+c=0\end{matrix}\right.\)
\(x=0;y=d\Rightarrow d=2\)
\(x=2;y=-2\Rightarrow8a+4b+2c+d=-2\)
\(\Rightarrow8a+4b+2=-2\Rightarrow\left\{{}\begin{matrix}12a+4b=0\\8a+4b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)
\(\Rightarrow y=x^3-3x^2+2\)
\(\Rightarrow y\left(-2\right)=-18\)
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
Câu 3:
Phương trình hoành độ giao điểm: \(-x=x^3\Leftrightarrow x^3+x=0\Leftrightarrow x\left(x^2+1\right)=0\Leftrightarrow x=0\).
Phương trình có \(1\) nghiệm do đó chọn C.
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
Câu 4:
\(2^{2x^2-7x+5}=32\)
\(\Leftrightarrow2^{2x^2-7x+5}=2^5\)
\(\Leftrightarrow2x^2-7x+5=5\)
\(\Leftrightarrow2x^2-7x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Suy ra \(x_1=0,x_2=\dfrac{7}{2}\).
\(x_1+4x_2=14\).
Chọn A.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
24.
\(log\left(a^3b^2\right)=loga^3+logb^2=3loga+2logb=3x+2y\)
25.
\(f'\left(x\right)=0\) có 2 nghiệm bội lẻ \(x=\left\{-\dfrac{3}{2};1\right\}\) nên hàm có 2 cực trị
26.
\(\lim\limits_{x\rightarrow\infty}\dfrac{x^2+3x-4}{x^2-16}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{1+\dfrac{3}{x}-\dfrac{4}{x^2}}{1-\dfrac{16}{x^2}}=1\)
\(\Rightarrow y=1\) là TCN của đồ thị hàm số
\(\lim\limits_{x\rightarrow-4}\dfrac{x^2+3x-4}{x^2-16}=\lim\limits_{x\rightarrow-4}\dfrac{\left(x-1\right)\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\lim\limits_{x\rightarrow-4}\dfrac{x-1}{x-4}=\dfrac{5}{8}\) hữu hạn
\(\Rightarrow x=-4\) không phải tiệm cận đứng
\(\lim\limits_{x\rightarrow4^+}\dfrac{x^2+3x-4}{x^2-16}=+\infty\Rightarrow x=4\) là 1 TCĐ
Vậy đồ thị hàm số có 2 tiệm cận
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
27.
\(y'=x^2-2x+2\)
\(y'\left(1\right)=1\)
\(y\left(1\right)=\dfrac{7}{3}\)
Phương trình tiếp tuyến có dạng:
\(y=1\left(x-1\right)+\dfrac{7}{3}\Leftrightarrow y=x+\dfrac{4}{3}\)
28.
ĐKXĐ: \(x>0\)
\(\log x\le1\)
\(\Rightarrow x\le10\)
Kết hợp ĐKXĐ ta được \(x\in(0;10]\)
29.
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
Do SAB vuông cân tại S \(\Rightarrow SH=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SH.a^2=\dfrac{a^3}{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 6 2019
\(y'=4x^3+3ax^2+2bx\)
\(y'=0\Rightarrow x\left(4x^2+3ax+b\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x^2+3ax+b=0\end{matrix}\right.\)
Xét \(g\left(x\right)=4x^2+3ax+b=0\) với \(\Delta=9a^2-16b\)
Hàm số luôn có 1 cực trị là \(x=0\), với \(y\left(0\right)=1\)
Dựa vào hình dáng đồ thị hàm bậc 4, để \(y\) đạt GTNN bằng 1 cũng chính là \(y\left(0\right)\) ta có các trường hợp sau:
- TH1: \(\Delta\le0\Rightarrow9a^2-16b\le0\Rightarrow b\ge\frac{9a^2}{16}\)
Khi đó \(S=a+b\ge a+\frac{9a^2}{16}=\frac{9}{16}\left(a+\frac{8}{9}\right)^2-\frac{4}{9}\ge-\frac{4}{9}\)
- TH2: \(g\left(x\right)=0\) có 2 nghiệm cùng âm \(x_1< x_2< 0\) và \(y\left(x_1\right)=1\)
\(\Rightarrow\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\\frac{-3a}{4}< 0\\x_1^4+ax_1^3+bx_1^2+1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a>0\\x_1^2+ax_1+b=0\end{matrix}\right.\)
Nói chung ta ko cần tìm tiếp, do \(a;b>0\Rightarrow a+b>0>-\frac{4}{9}\)
TH3: \(g\left(x\right)=0\) có 2 nghiệm cùng dương \(0< x_1< x_2\) và \(y\left(x_2\right)=1\)
\(\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\-\frac{3a}{4}>0\\y\left(x_2\right)=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a< 0\end{matrix}\right.\)
\(y\left(x_2\right)=x_2^4+ax_2^3+bx_2^2+1=1\)
\(\Leftrightarrow x_2^2+ax_2+b=0\)
\(\Rightarrow\left\{{}\begin{matrix}4x_2^2+3ax_2+b=0\\x_2^2+ax_2+b=0\end{matrix}\right.\) \(\Rightarrow3x_2^2+2ax_2=0\Rightarrow x_2=-\frac{2a}{3}\)
\(\Rightarrow\frac{4a^2}{9}-\frac{2a^2}{3}+b=0\Rightarrow b=\frac{2a^2}{9}\)
\(\Rightarrow S=a+b=\frac{2a^2}{9}+a=\frac{2}{9}\left(a+\frac{9}{4}\right)^2-\frac{9}{8}\ge-\frac{9}{8}\)
So sánh 2 giá trị \(-\frac{4}{9}\) và \(-\frac{9}{8}\) ta được \(S_{min}=-\frac{9}{8}\) khi \(\left\{{}\begin{matrix}a=-\frac{9}{4}\\b=\frac{9}{8}\end{matrix}\right.\)
TA
11 tháng 8 2021
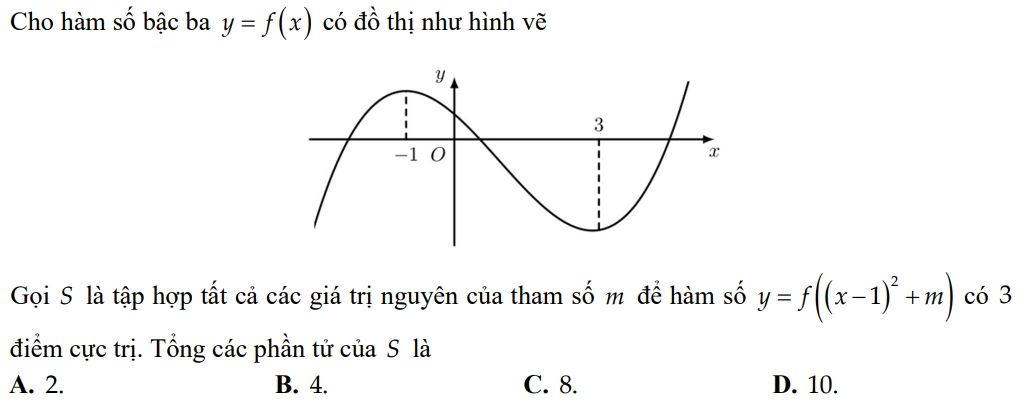
B, Đồ thị y thì nhìn vào dáng điệu, đồ thị y' thì chú ý trục hoành
H
29 tháng 5 2023
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
x-26,789 =12,34+33,45
x-26,789=45,79
x=45,79+26,789
x=72,579