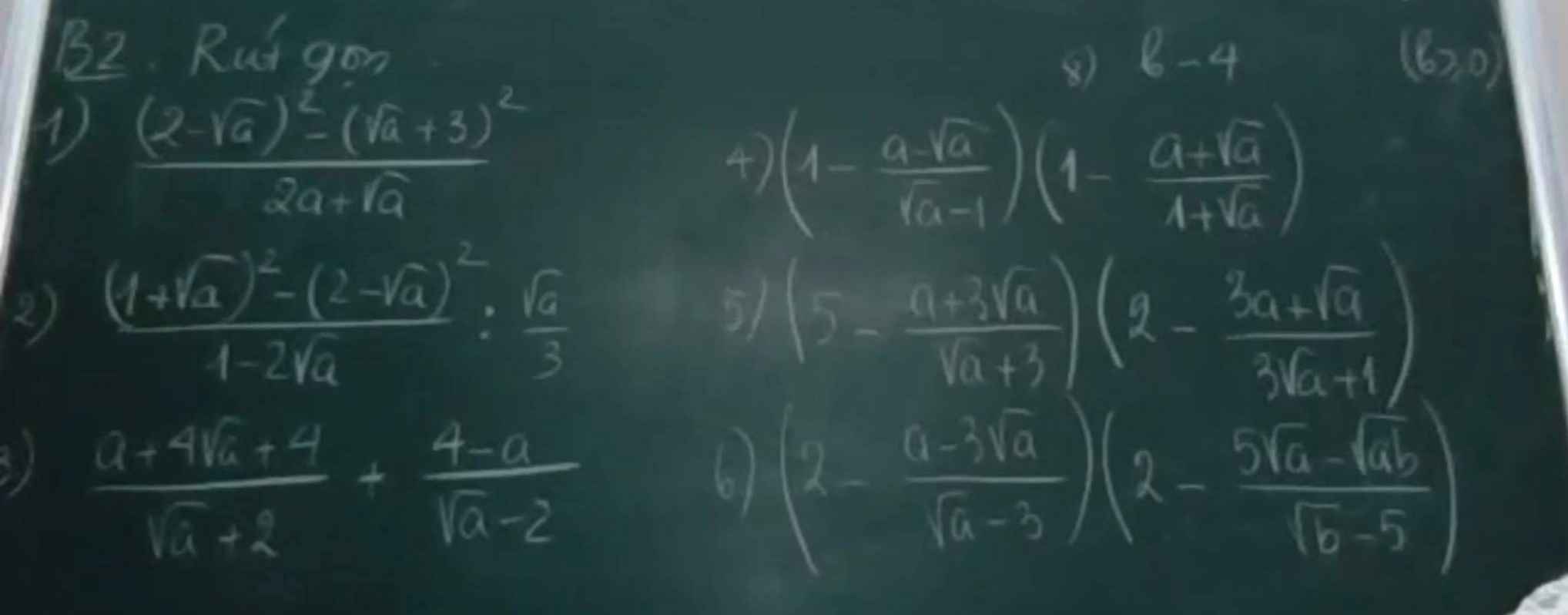K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2021
2b)
xét vế trái ta có
=\(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{x^2y}+\sqrt{xy^2}}{\sqrt{xy}}\) \(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)=x-y
3b)
để A<0 \(\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\)\(\Rightarrow\sqrt{x}< 1\)\(\Rightarrow x< 1\)
21 tháng 8 2021
a: Ta có: \(\sqrt{9x^2-6x+1}=5\)
\(\Leftrightarrow\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
ND
Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
0
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
TR
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
8 tháng 2 2022
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun
AT
3 tháng 7 2021
2) \(\dfrac{\left(1+\sqrt{a}\right)^2-\left(2-\sqrt{a}\right)^2}{1-2\sqrt{a}}:\dfrac{\sqrt{a}}{3}\left(a>0,a\ne\dfrac{1}{4}\right)\)
\(=\dfrac{\left(1+\sqrt{a}-2+\sqrt{a}\right)\left(1+\sqrt{a}+2-\sqrt{a}\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}\)
\(=\dfrac{3.\left(2\sqrt{a}-1\right)}{1-2\sqrt{a}}.\dfrac{3}{\sqrt{a}}=-\dfrac{9}{\sqrt{a}}\)
5) \(\left(5-\dfrac{a+3\sqrt{a}}{\sqrt{a}+3}\right)\left(2-\dfrac{3a+\sqrt{a}}{3\sqrt{a}+1}\right)\left(a\ge0\right)\)
\(=\left(5-\dfrac{\sqrt{a}\left(\sqrt{a}+3\right)}{\sqrt{a}+3}\right)\left(2-\dfrac{\sqrt{a}\left(3\sqrt{a}+1\right)}{3\sqrt{a}+1}\right)\)
\(=\left(5-\sqrt{a}\right)\left(2-\sqrt{a}\right)=10-7\sqrt{a}+a\)
6) \(\left(2-\dfrac{a-3\sqrt{a}}{\sqrt{a}-3}\right)\left(2-\dfrac{5\sqrt{a}-\sqrt{ab}}{\sqrt{b}-5}\right)\left(a,b\ge0,a\ne9,b\ne25\right)\)
\(=\left(2-\dfrac{\sqrt{a}\left(\sqrt{a}-3\right)}{\sqrt{a}-3}\right)\left(2+\dfrac{\sqrt{a}\left(\sqrt{b}-5\right)}{\sqrt{b}-5}\right)\)
\(=\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)=4-a\)
3 tháng 7 2021
3) Ta có: \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)
\(=\sqrt{a}+2-\sqrt{a}-2\)
=0
22 tháng 3 2023
a: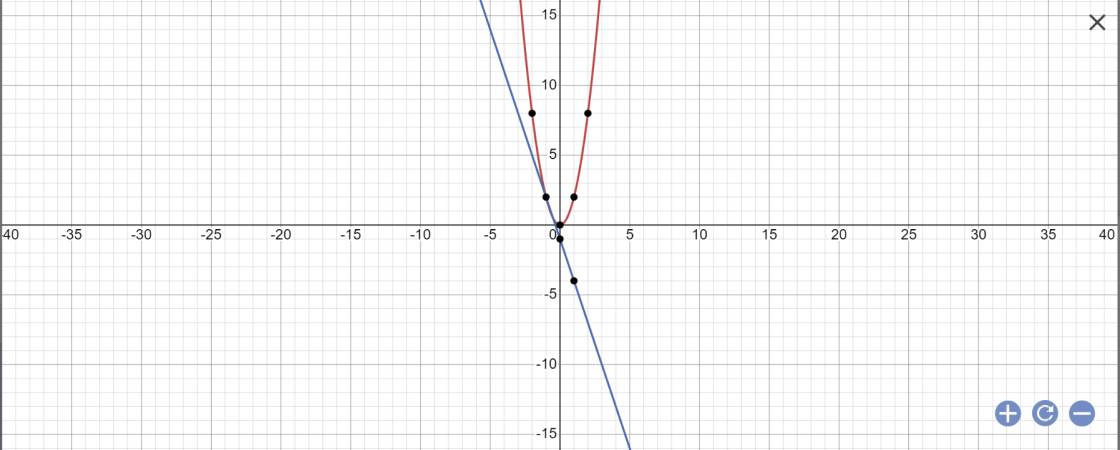 
b: PTHĐGĐ là:
2x^2+3x+1=0
=>x=-1 hoặc x=-1/2
=>y=2 hoặc y=1/2
Y
22 tháng 3 2023
\(a,\) Tự vẽ nha
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x-1\)
\(\Leftrightarrow2x^2+3x+1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-1\end{matrix}\right.\)
Thay \(x_1=-\dfrac{1}{2}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
Thay \(x_2=-1\) vào \(\left(d\right):y=-3x-1\Rightarrow y=-3.\left(-1\right)-1=2\)
Vậy tọa độ của 2 đồ thị hàm số là \(A\left(-\dfrac{1}{2};\dfrac{1}{2}\right);B\left(-1;2\right)\)
Y
22 tháng 3 2023
\(a,\) Tự vẽ nhaa
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x+1\)
\(\Leftrightarrow2x^2+3x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-3+\sqrt{17}}{4}\\x_2=\dfrac{-3-\sqrt{17}}{4}\end{matrix}\right.\)
Thay \(x_1=\dfrac{-3+\sqrt{17}}{4}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(\dfrac{-3+\sqrt{17}}{4}\right)=\dfrac{-3+\sqrt{17}}{2}\)
Thay \(x_2=\dfrac{-3-\sqrt{17}}{4}\) vào \(\left(d\right):y=-3x+1\Rightarrow y=-3.\left(\dfrac{-3-\sqrt{17}}{4}\right)+1=\dfrac{13+3\sqrt{17}}{4}\)
Vậy toa độ giao điểm của 2 đồ thị hàm số là
\(A\left(\dfrac{-3+\sqrt{17}}{4};\dfrac{-3+\sqrt{17}}{2}\right)\) và \(B\left(\dfrac{-3-\sqrt{17}}{4};\dfrac{13+3\sqrt{17}}{4}\right)\)
14 tháng 4 2021
Gọi vận tốc xe máy là x ( x > 0, km/h )
vận tốc ô tô là x + 10 km/h
Thời gian xe máy đi từ A -> B là : \(\dfrac{100}{x}\)giờ
Thời gian ô tô đi từ A -> B là : \(\dfrac{100}{x+10}\)giờ
Do ô tô và xe máy suất phát cùng lúc, quãng đường AB ko đổi và ô tô đến B trước xe máy 30 phút = 1/2 giờ
nên ta có phương trình : \(\dfrac{100}{x}-\dfrac{100}{x+10}=\dfrac{1}{2}\)
giải phương trình ta thu được : \(x=40\left(chon\right);x=-50\left(loai\right)\)
Vậy vận tốc xe máy là 40 km/h
vận tốc ô tô là 40 + 10 = 50 km/h
14 tháng 4 2021
Câu IV:
Gọi vận tốc của xe máy là x(km/h)(Điều kiện: x>0)
Vận tốc của xe ô tô là: x+10(km/h)
Thời gian xe máy đi từ A đến B là: \(\dfrac{100}{x}\left(h\right)\)
Thời gian ô tô đi từ A đến B là: \(\dfrac{100}{x+10}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{100}{x}-\dfrac{100}{x+10}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{200\left(x+10\right)}{2x\left(x+10\right)}-\dfrac{200x}{2x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{2x\left(x+10\right)}\)
Suy ra: \(x^2+10x=200x+2000-200x\)
\(\Leftrightarrow x^2+50x-40x-2000=0\)
\(\Leftrightarrow x\left(x+50\right)-40\left(x+50\right)=0\)
\(\Leftrightarrow\left(x+50\right)\left(x-40\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+50=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-50\left(loại\right)\\x=40\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc của xe máy là 40km/h
Vận tốc của ô tô là 50km/h
