
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2^{x+2}-2^x=96\)
\(\Rightarrow2^x.2^2-2^x=96\)
\(\Rightarrow2^x\left(2^2-1\right)=96\)
\(\Rightarrow2^x.3=96\)
\(\Rightarrow2^x=32\Rightarrow2^x=2^5\Rightarrow x=5\)


Bài 1:
Ta có: \(4x^5y^2-3x^3y+7x^3y+ax^5y^2\)
\(=\left(a+4\right)\cdot x^5y^2+4x^3y\)
Để đa thức có bậc bằng 4 thì a+4=0
hay a=-4
Vậy: a=-4

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó; ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF và ME=MF
hay ΔMEF cân tại M
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

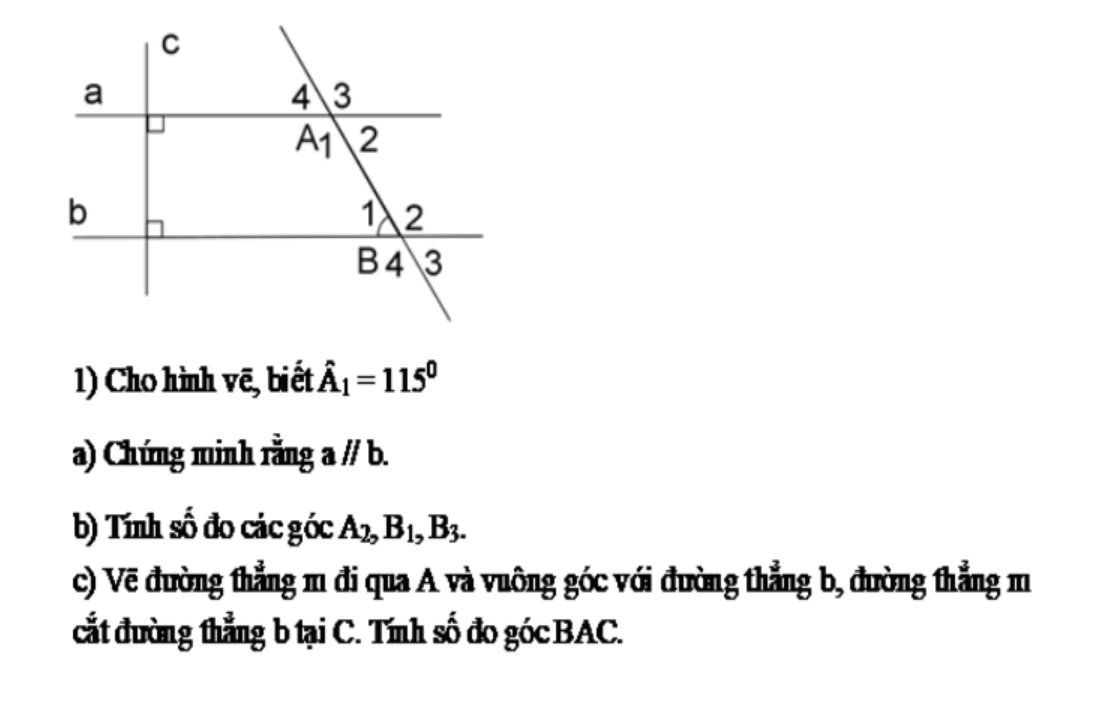
a) Ta có: a⊥c,b⊥c
=> a//b
b) \(\widehat{A_2}+\widehat{A_1}=180^0\)(kề bù)
\(\Rightarrow\widehat{A_2}=180^0-115^0=65^0\)
\(\widehat{B_1}=\widehat{A_2}=65^0\)(so le trong do a//b)
\(\Rightarrow\widehat{B_1}=\widehat{B_3}=65^0\)(đối đỉnh)
MN ơi giải giúp em bài này với : a) chứng tỏ tia A3=B1 b) chứng tỏ A3 + B4= 180 độ c) chứng tỏ A1=B1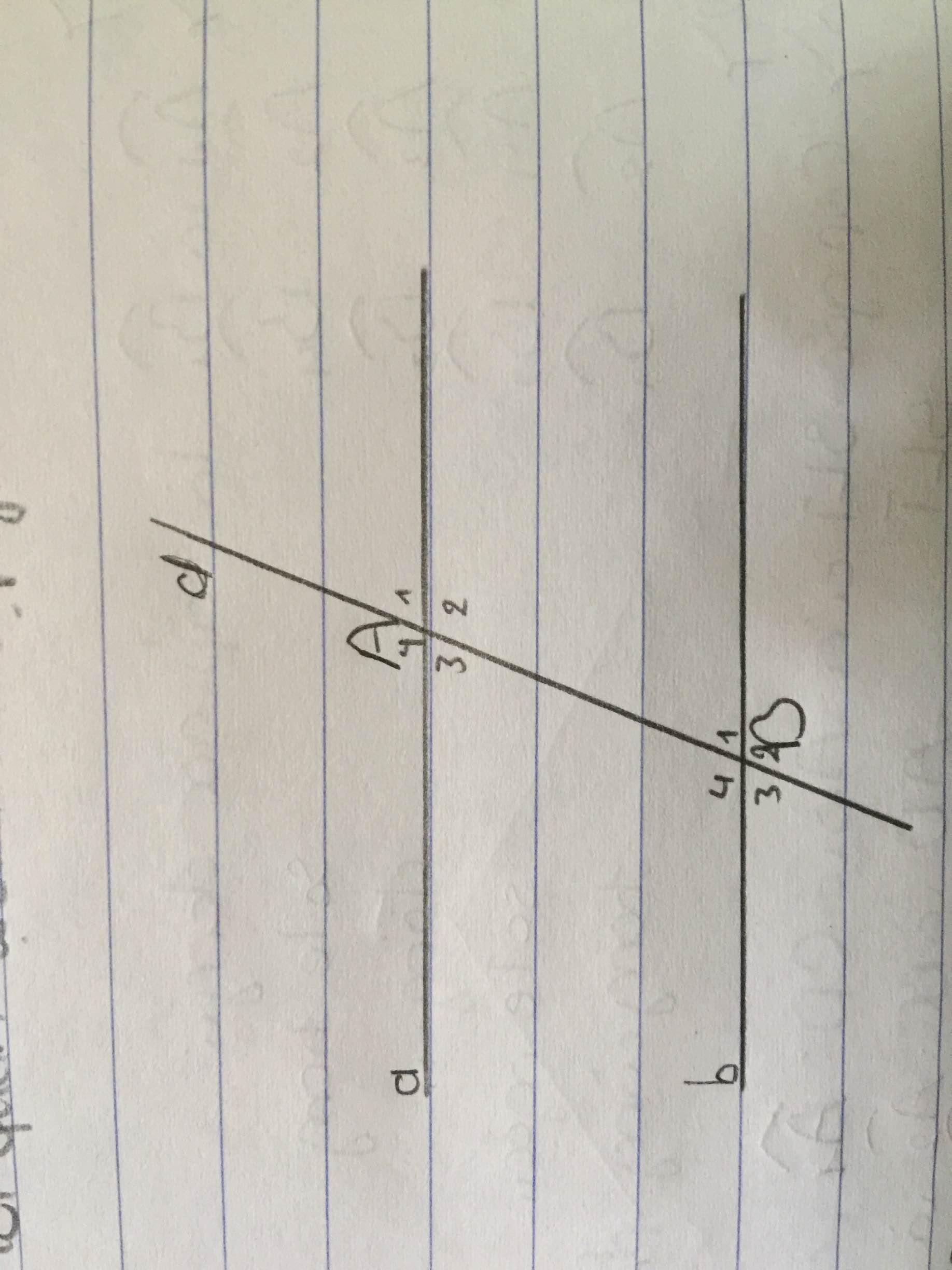


a) \(x-\dfrac{1}{4}=-\dfrac{1}{6}\Leftrightarrow x=-\dfrac{1}{6}+\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{12}\)
b) \(\dfrac{2}{5}x-\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\Leftrightarrow\dfrac{2}{5}x=\dfrac{1}{9}+\dfrac{1}{9}\Leftrightarrow\dfrac{2}{5}x=\dfrac{2}{9}\Leftrightarrow x=\dfrac{5}{9}\)
c) \(\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3-\dfrac{1}{3}\\x=-3-\dfrac{1}{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
\(\left(a\right)\)
\(x-\dfrac{1}{4}=\dfrac{-1}{6}\)
\(x=\dfrac{1}{12}\)
/\(x+\dfrac{1}{3}\)/=3
=> \(x+\dfrac{1}{3}=3\) hoặc \(-x-\dfrac{1}{3}=3\)
=> x=\(\dfrac{8}{3}\) hoặc x= \(\dfrac{-10}{3}\)

a) \(\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{7}\right)=\dfrac{3}{7}-\dfrac{5}{2}-\dfrac{3}{7}=-\dfrac{5}{2}\)
b) \(B=\dfrac{4^2.2^3}{2^6}=\dfrac{\left(2^2\right)^2.2^3}{2^6}=\dfrac{2^4.2^3}{2^6}=\dfrac{2^7}{2^6}=2\)
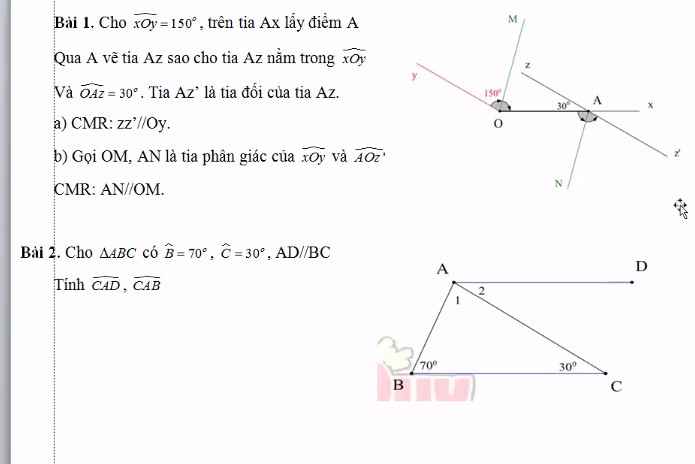


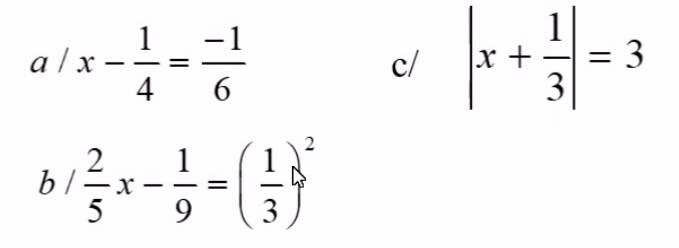

a.Xét tam giác vuông AED và tam giác vuông AFD, có:
A: góc chung
AD: cạnh chung
Vậy tam giác vuông AED = tam giác vuông AFD ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
b.Xét tam giác vuông BDE và tam giác vuông CDF, có:
góc B = góc C ( gt )
DE = DF ( cmt )
Vậy tam giác vuông BDE = tam giác vuông CDF ( góc nhọn. cạnh góc vuông )
c. ta có: AD là đường phân giác trong tam giác cân ABC cũng là đường trung trực
=> AD là đường trung trực của BC
Chúc bạn học tốt!!!
camon bn nhiều ạ