
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




nhờ giải hình thì chụp cả hình đi chứ nhiều người lười vẽ lắm.
chẳng hạn như mình.....

Bài 2:
a: Vì (d) có hệ số góc là 3 nên a=3
Vậy: (d): y=3x+b
Thay x=1 và y=0 vào (d), ta được:
b+3=0
hay b=-3
b: Vì (d)//y=0,5x-2 nên a=0,5
Vậy: (d): y=0,5x+b
Thay x=0 và y=2 vào (d), ta được:
b=2


a: Thay x=36 vào P, ta được:
\(P=\dfrac{6+1}{6-2}=\dfrac{7}{4}\)
b: Thay \(x=6-2\sqrt{5}\) vào P, ta được:
\(P=\dfrac{\sqrt{5}-1+1}{\sqrt{5}-1-2}=\dfrac{\sqrt{5}}{\sqrt{5}-3}=\dfrac{-5-3\sqrt{5}}{4}\)

a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m+2\right)x-2m\)
\(\Leftrightarrow x^2-\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2-8m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\)
mà \(\left(m-2\right)^2\ge0\)
nên \(m-2\ne0\)
hay \(m\ne2\)
Vậy: Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(m\ne2\)

\(P=\left[\dfrac{a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a+\sqrt{a}}{a-1}\right]:\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{1}{\sqrt{a}-1}\right)\) (đk:\(a\ge0;a\ne1\))
\(=\left[\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right]:\dfrac{\sqrt{a}-1+\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{\sqrt{a}-1}\right).\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{2\sqrt{a}}\)
\(=\dfrac{1}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{2\sqrt{a}}=\dfrac{\sqrt{a}+1}{2\sqrt{a}}\)
2) \(\dfrac{1}{P}\ge\dfrac{\sqrt{a}+9}{8}\)
\(\Leftrightarrow\dfrac{2\sqrt{a}}{\sqrt{a}+1}\ge\dfrac{\sqrt{a}+9}{8}\)
\(\Leftrightarrow16\sqrt{a}\ge\left(\sqrt{a}+9\right)\left(\sqrt{a}+1\right)\)
\(\Leftrightarrow a-6\sqrt{a}+9\le0\)
\(\Leftrightarrow\left(\sqrt{a}-3\right)^2\le0\)
Dấu "=" xảy ra khi \(\sqrt{a}-3=0\Leftrightarrow a=9\) (tm)
Vậy...
1) ĐKXĐ: \(a\ge0;a\ne1\)
\(P=\left[\dfrac{a+\sqrt{a}+2\sqrt{a}+2}{\left(\sqrt{a}+2\right).\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}.\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right).\left(\sqrt{a}+1\right)}\right]\)\(:\left[\dfrac{\sqrt{a}-1+\sqrt{a}+1}{\left(\sqrt{a}-1\right).\left(\sqrt{a}+1\right)}\right]\)
\(\Leftrightarrow P=\left[\dfrac{\sqrt{a}.\left(\sqrt{a}+1\right)+2.\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+2\right).\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}}{\sqrt{a}-1}\right]\)\(:\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right).\left(\sqrt{a}+1\right)}\)
\(\Leftrightarrow P=\left[\dfrac{\left(\sqrt{a}+2\right).\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+2\right).\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}}{\sqrt{a}-1}\right].\dfrac{\left(\sqrt{a}-1\right).\left(\sqrt{a}+1\right)}{2\sqrt{a}}\)
\(\Leftrightarrow P=\dfrac{\sqrt{a}+1-\sqrt{a}}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right).\left(\sqrt{a}+1\right)}{2\sqrt{a}}\)
\(\Leftrightarrow P=\dfrac{\sqrt{a}+1}{2\sqrt{a}}\)
2) Có : \(\dfrac{1}{P}\ge\dfrac{\sqrt{a}+9}{8}\)
\(\Leftrightarrow\dfrac{2\sqrt{a}}{\sqrt{a}+1}\ge\dfrac{\sqrt{a}+9}{8}\)
\(\Leftrightarrow\dfrac{2\sqrt{a}}{\sqrt{a}+1}-\dfrac{\sqrt{a}+9}{8}\ge0\)
\(\Leftrightarrow\dfrac{16\sqrt{a}-\left(\sqrt{a}+9\right).\left(\sqrt{a}+1\right)}{8.\left(\sqrt{a}+1\right)}\ge0\)
\(\Leftrightarrow\dfrac{16\sqrt{a}-a-10\sqrt{a}-9}{8.\left(\sqrt{a}+1\right)}\ge0\)
\(\Leftrightarrow\dfrac{-\left(a-6\sqrt{a}+9\right)}{8.\left(\sqrt{a}+1\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{a}-3\right)^2}{8.\left(\sqrt{a}+1\right)}\le0\)
Vì \(\sqrt{a}\ge0\Rightarrow8.\left(\sqrt{a}+1\right)>0\) mà \(\left(\sqrt{a}-3\right)^2\) \(\ge0\)
\(\Rightarrow\) \(\dfrac{\left(\sqrt{a}-3\right)^2}{8.\left(\sqrt{a}+1\right)}=0\) \(\Rightarrow\left(\sqrt{a}-3\right)^2=0\) \(\Leftrightarrow\sqrt{a}-3=0\Leftrightarrow\sqrt{a}=3\Leftrightarrow a=9\)
Vậy để\(\dfrac{1}{P}\ge\dfrac{\sqrt{a}+9}{8}\) thì \(a=9\)







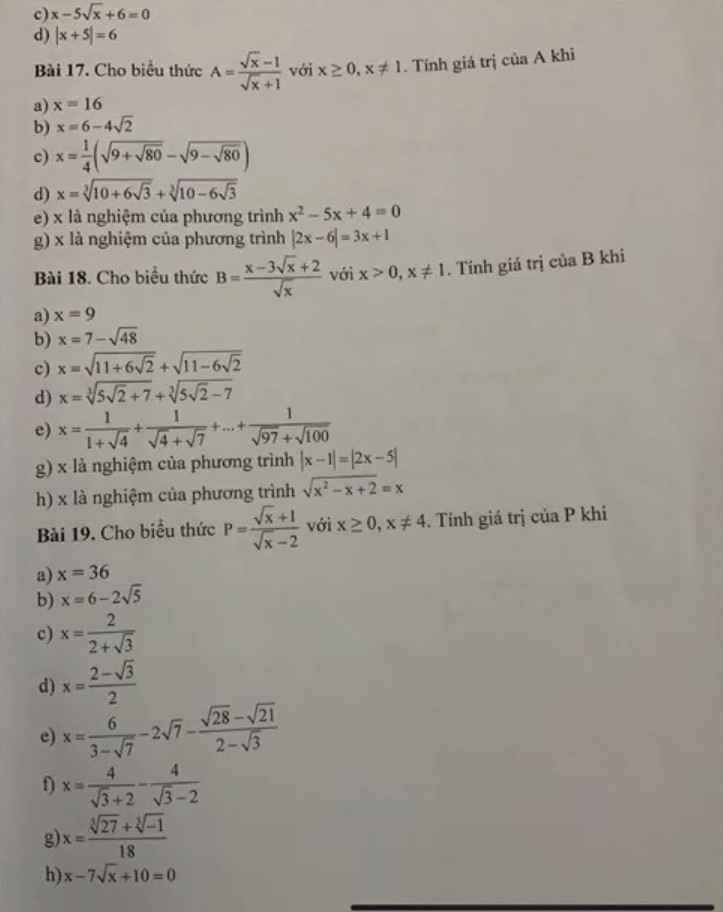 giải hộ mình bài 19 ạ
giải hộ mình bài 19 ạ

