K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(\left\{{}\begin{matrix}3x+1< x-7\\1-2x>x+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x< -8\\3x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x< 0\end{matrix}\right.\) \(\Rightarrow x< -4\)
Vậy nghiệm của hệ là \(S=\left(-\infty;-4\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
2.
Xét BPT: \(\left(x+3\right)\left(4-x\right)>0\Leftrightarrow-3< x< 4\) \(\Rightarrow D_1=\left(-3;4\right)\)
Xét BPT: \(x< m-1\) \(\Rightarrow D_2=\left(m-1;+\infty\right)\)
Hệ có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Leftrightarrow m-1< 4\)
\(\Leftrightarrow m< 5\)
3.
\(\dfrac{\pi}{24}=\dfrac{180^0}{24}=7^030'\)
4.
\(x^2+y^2-x+y+4=0\) không phải đường tròn
Do \(\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2-4< 0\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
5.
\(f\left(x\right)=ax^2+bx+c\) có \(\left\{{}\begin{matrix}a\ne0\\\Delta=b^2-4ac< 0\end{matrix}\right.\) thì \(f\left(x\right)\) không đổi dấu trên R
6.
\(sin2020a=sin\left(2.1010a\right)=2sin1010a.cos1010a\)
7.
Công thức B sai
\(cos^2a+sin^2a=1\) , không phải \(cos2a\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)
NN
1
HP
19 tháng 3 2021
ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
DT
0
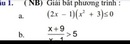
a. ta có \(x^2+3>0\text{ nên }\left(2x-1\right)\left(x^2+1\right)\le0\Leftrightarrow2x-1\le0\Leftrightarrow x\le\frac{1}{2}\)
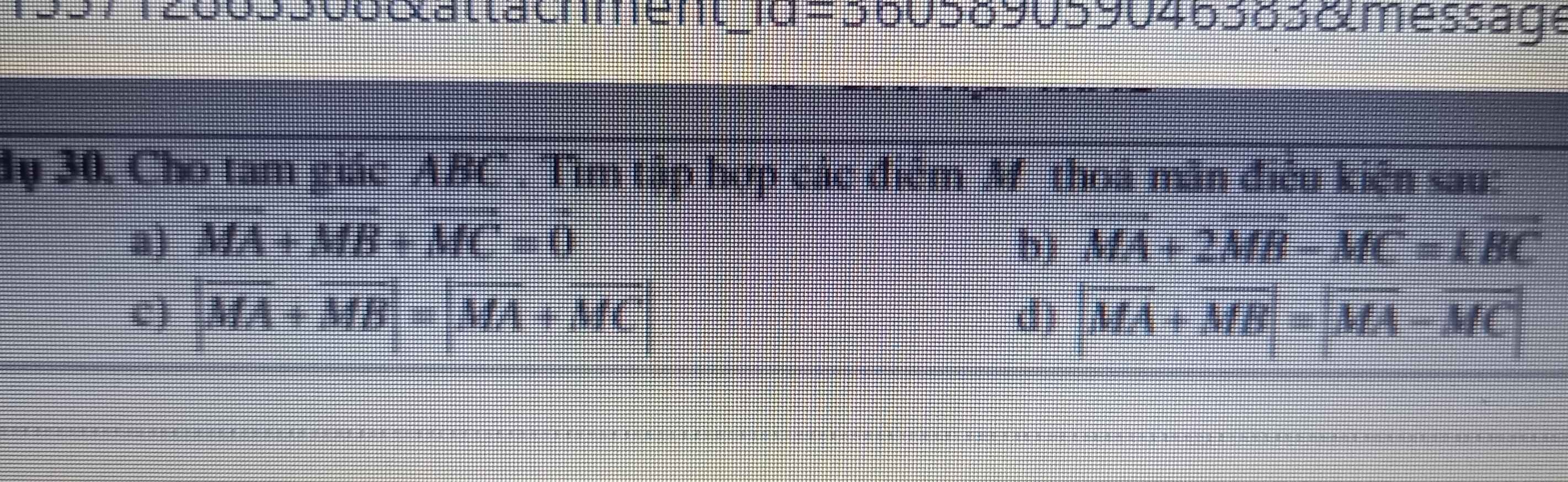
b. ta có \(\frac{x+9}{x-1}>5\Leftrightarrow\frac{x+9-5x+5}{x-1}>0\Leftrightarrow\frac{14-4x}{x-1}>0\)
\(\hept{\begin{cases}14-4x>0\\x-1>0\end{cases}\Leftrightarrow\frac{7}{2}>x>1}\) hoặc \(\hept{\begin{cases}14-4x< 0\\x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>\frac{7}{2}\\x< 1\end{cases}}}\) vô lí
vậy \(1< x< \frac{7}{2}\)
a) \(\left(2x-1\right)\left(x^2+3\right)\le0\)
\(\Leftrightarrow\hept{\begin{cases}2x-1\le0\\x^2+3\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1\ge0\\x^2+3\le0\end{cases}}\)
mà \(x^2+3>0\forall x\)
nên \(\hept{\begin{cases}2x-1\le0\\x^2+3>0\end{cases}}\)
\(\Leftrightarrow x\le\frac{1}{2}\)
Vậy nghiệm của BPT là \(x\le\frac{1}{2}\)
b) Đề bị che mất mẫu số nên không đọc được đề =))