K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
1
VD
4
NH
mn giúp mình vs đang cần rất gấp!!! ;-;
1
15 tháng 11 2021
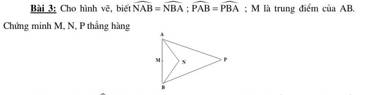
Bài 3:
Áp dụng tc dtsnb:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+2y-z}{5+3\cdot2-4}=\dfrac{63}{7}=9\\ \Rightarrow\left\{{}\begin{matrix}x=45\\y=27\\z=36\end{matrix}\right.\)
18 tháng 3 2021
Câu 7
a,Xét \(\Delta ICA\) và \(\Delta ICB\) ta có :
\(AC=CB\) ( do \(\Delta ABC\) cân tại \(C\) nên 2 cạnh bên bằng nhau )
\(\widehat{CAI} = \widehat{CBI}\) ( hai góc ở đáy )
\(AI=IB \)(do \(I\) là trung điểm của \(AB\))
\(\Rightarrow\Delta ICA=\Delta ICB\left(c.g.c\right)\)
b,Ta có \(CI \) là trung tuyến suất phát từ đỉnh \(C\)
\(\Rightarrow CI\perp AB\)(tính chất đường trung tuyến trong tam giác cân)
c, Áp dụng định lý \(Pi-ta-go\) vào tam giác vuông \(CIA\) ta có :
\(AC^2=CI^2+IA^2\Rightarrow AC=\sqrt{CI^2+IA^2}\)
\(\Leftrightarrow AC=\sqrt{12^2+5^2}=13\)
\(\Rightarrow AC=BC=13\left(cm\right)\)
Chu vi \(\Delta ABC\) là
\(AC+CB+AB=13+13+10=36\left(cm\right)\)
TK
0
14 tháng 4 2021
Gọi gốc là điểm A, chỗ gãy là B, ngọn đã gãy là điểm C
Xét tam giác ABC vuông tại A có: AB = 6m, BC = 16m - 6m = 10m
=> AB2 + AC2 = BC2 (Định lý Py-ta-go)
Thay: 62 + AC2 = 102
36 + AC2 = 100
AC2 = 100 - 36 = 64
AC = 8 (m)
Vậy khoảng cách từ gốc đến ngọn cây bị gãy là 8 mét
Nếu đúng hãy K cho mình nha
Học tốt nhé
LD
1
26 tháng 5 2022
Xét tam giác NAB cân tại N, có M là trung điểm của AB suy ra NM vuông góc với AB (1)
Xét tam giác APB cân tại P, có M là trung điểm của AB suy ra MP vuông góc với AB (2)
Từ (1,2) suy ra M, N, P thẳng hàng
Muốn giải đáp các thắc mắc tới toán , vật lý vui lòng chat trức tiếp
khó nhìn quá :) câu 27 sao câu A,B.C giống nhau z :)
Câu 28: C
Câu 29: B,D