TT
GIẢI GIÚP MÌNH VỚI Ạ!💚💚💚
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AM
0
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
N
1
HN
11 tháng 12 2021
a) \(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(\Leftrightarrow A=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4}{x-1}\)
b) \(A=7\) \(\Leftrightarrow\dfrac{4}{x-1}=7\)
\(\Leftrightarrow7x-7=4\) \(\Leftrightarrow7x=11\Leftrightarrow x=\dfrac{11}{7}\left(TM\right)\)
11 tháng 12 2021
\(a,A=\dfrac{x+2\sqrt{x}-3-x+2\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{4}{x-1}\\ b,A=7\Leftrightarrow x-1=\dfrac{4}{7}\Leftrightarrow x=\dfrac{11}{7}\left(tm\right)\)
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
U
1
8 tháng 6 2021
Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....
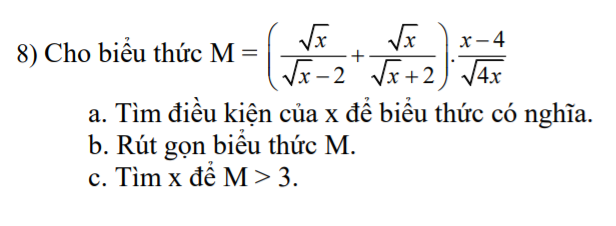
@Nguyễn Quang Định