Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng hệ thức lượng:
\(AH^2=BH.CH=4.9=36\)
\(\Rightarrow AH=6\left(cm\right)\)
\(BC=4+9=13\left(cm\right)\)
- Nếu \(BH=4\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow AB=\sqrt{4.13}=2\sqrt{13}\) (cm)
\(sinC=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\Rightarrow C\approx33^041'\)
- Nếu \(BH=9\Rightarrow AB=\sqrt{BH.BC}=\sqrt{9.13}=3\sqrt{13}\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}=\dfrac{3\sqrt{13}}{13}\Rightarrow C\approx56^019'\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.6.13=39\left(cm^2\right)\)
(Vì đề không nói rõ BH, CH bằng 4 hay 9 nên mình cho BH = 4 và CH = 9 nhé!)
Áp dụng HTL vào \(\Delta ABC\) vuông tại A đường cao AH:
\(AH^2=BH\cdot HC\Leftrightarrow AH=\sqrt{BH\cdot HC}=\sqrt{4\cdot9}=6\left(cm\right)\)
Áp dụng HTL vào \(\Delta ABH\) vuông tại H:
\(AB^2=AH^2+BH^2\Leftrightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
Áp dụng tslg vào \(\Delta ABC\) vuông tại A, đường cao AH:
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{4+9}\approx34^0\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{13}\cdot\left(\sqrt{13^2-\left(2\sqrt{13}\right)^2}\right)_{Pytago}=39cm^2\)


Gọi x là chiều cao của tam giác ; y là cạnh đáy của tam giác (x,y > 0 )
* chiều cao bằng 3/4 đáy:
x = 3/4y
=> x - 3/4y = 0 (1)
* Nếu chiều cao tăng thêm...tăng thêm 9m^2:
1/2(y-2)(x+3) = 1/2xy + 9 (sau đó bạn tự giải phương trình nha) (2)
Từ (1),(2) suy ra chiều cao là 12m , cạnh đáy là 16m

Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....



\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)

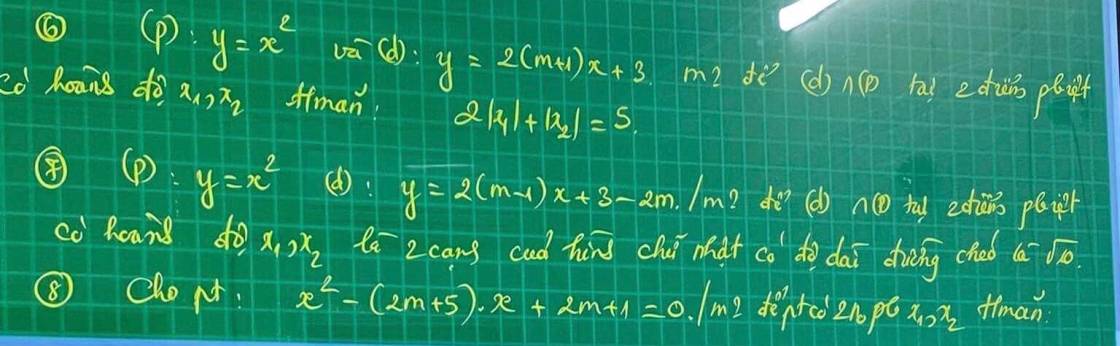



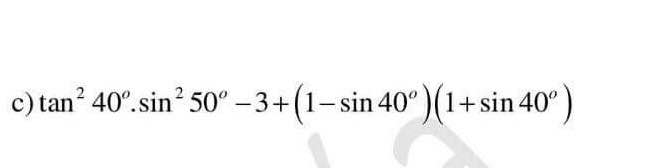 mọi người giải giúp em câu này vs ạ
mọi người giải giúp em câu này vs ạ