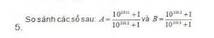Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu1:a) \(\left(\dfrac{-2}{3}\right)^2\)+\(\dfrac{-7}{6}\)\(\div\dfrac{3}{8}\)=\(\dfrac{4}{9}\)+\(\dfrac{-7}{6}\times\dfrac{8}{3}\)=\(\dfrac{4}{9}\)+\(\dfrac{-28}{9}\)=\(\dfrac{-24}{9}\)=\(\dfrac{-8}{3}\)
b)=\(\dfrac{-1}{10}\)\(\times\dfrac{9}{2}\)\(-\)\(\dfrac{1}{4}\)=\(\dfrac{-9}{20}-\dfrac{5}{20}\)=\(\dfrac{-14}{20}\)=\(\dfrac{-7}{10}\)
Câu 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y+z}{4+5+7}=\dfrac{-32}{16}=-2\)
Do đó: x=-8; y=-10; z=-14

( 2x + 1) 3 = -0,001
(2x+1)3=(-0,1)3
=>2x+1=-0,1
2x=-0,1-1
2x=\(\frac{-1}{10}-\frac{10}{10}\)
2x=\(\frac{-11}{10}\)
x=\(\frac{-11}{10}:2\)
x=\(\frac{-11}{10}.\frac{1}{2}\)
x=\(\frac{-11}{20}\)


Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)

`Answer:`
Ảnh mờ quá nên mình có làm sai đề thì bạn bảo nhé.
\(A=\frac{10^{2011}+1}{20^{2012}+1}\)
\(\Rightarrow10A=\frac{10^{2012}+10}{10^{2012}+1}=1+\frac{9}{10^{2012}+1}\)
\(B=\frac{10^{2012}+1}{10^{2013}+1}\)
\(\Rightarrow10B=\frac{10^{2013}+10}{10^{2013}+1}=1+\frac{9}{10^{2013}+1}\)
Mà \(10^{2012}+1< 10^{2013}+1\)
\(\Rightarrow\frac{9}{10^{2012}+1}>\frac{9}{10^{2013}+1}\)
\(\Rightarrow1+\frac{9}{10^{2012}+1}>1+\frac{9}{10^{2013}+1}\) hay \(10A>10B\)
Vậy `A>B`
B<102012+1+9102013+1+9=102012+10102013+10=10(102011+1)10(102012+1)=102011+1102012+1=A
Vậy A > B

Câu 4:
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
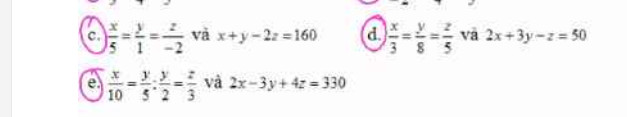 giải giúp mình 3 câu này
giải giúp mình 3 câu này