K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PL
2
30 tháng 8 2021
Câu 3:
a: Ta có: \(2x\left(3x-1\right)-\left(x-3\right)\left(6x+2\right)\)
\(=6x^2-2x-6x^2-2x+18x+6\)
=14x+6
b: Ta có: \(2x\left(x+7\right)-3x\left(x+1\right)\)
\(=2x^2+14x-3x^2-3x\)
\(=-x^2+11x\)
30 tháng 8 2021
Câu 2:
a: Ta có: \(\left(-8x^5+12x^3-16x^2\right):4x^2\)
\(=-8x^5:4x^2+12x^3:4x^2-16x^2:4x^2\)
\(=-2x^3+3x-4\)
b: Ta có: \(\left(12x^3y^3-18x^2y+9xy^2\right):6xy\)
\(=12x^3y^3:6xy-18x^2y:6xy+9xy^2:6xy\)
\(=2x^2y^2-3x+\dfrac{3}{2}y\)
c: Ta có: \(\dfrac{x^3-11x^2+27x-9}{x-3}\)
\(=\dfrac{x^3-3x^2-8x^2+24x+3x-9}{x-3}\)
\(=x^2-8x+3\)
d: Ta có: \(\dfrac{6x^4-13x^3+7x^2-x-5}{3x+1}\)
\(=\dfrac{6x^4+2x^3-15x^3-5x^2+12x^2+4x-5x-\dfrac{5}{3}-\dfrac{10}{3}}{3x+1}\)
\(=2x^3-5x^2+4x-\dfrac{5}{3}-\dfrac{\dfrac{10}{3}}{3x+1}\)
6 tháng 9 2021
\(\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)\left(-2+x^2\right)=1\)
\(\Leftrightarrow\left(-2+x^2\right)^5=1\)
\(\Leftrightarrow-2+x^2=1\)
\(\Leftrightarrow x^2=3\Leftrightarrow x=\pm\sqrt{3}\)
YL
11 tháng 9 2021
cho tam giác abc có ba góc nhọn (AB<AC) gọi ah là đường cao và M, N, P lần lượt là trung điểm AB,AC và BC. Gọi d là đối xứng của h qua m
a)c/m tứ giác DAHB là hcn
b) tìm đk của tam giác của ABC để AMPN là hcn
Đề nè mng:<<
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
a.
Ta có D đối xứng H qua M \(\Rightarrow M\) là trung điểm DH
Mà M là trung điểm AB theo giả thiết
\(\Rightarrow\) Tứ giác DAHB là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường)
Lại có \(AH\perp BC\) (gt) \(\Rightarrow\widehat{AHB}=90^0\)
\(\Rightarrow\) DAHB là hình chữ nhật (hbh có 1 góc vuông)
b.
N là trung điểm AC, P là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}AB\\NP||AB\end{matrix}\right.\)
M là trung điểm AB \(\Rightarrow AM=\dfrac{1}{2}AB\) \(\Rightarrow\left\{{}\begin{matrix}NP=AM\\NP||AM\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác AMPN là hình bình hành (cặp cạnh đối song song và bằng nhau)
Để AMPN là hình chữ nhật \(\Rightarrow\widehat{BAC}=90^0\)
\(\Rightarrow\) Tam giác ABC là tam giác vuông tại A
YL
7
KK
7 tháng 9 2021
a. -2x(x3 - 3x2 - x + 1)
= -2x4 + 6x3 + 2x2 - 2x
c. 3x2(2x3 - x + 5)
= 6x5 - 3x3 + 15x2
7 tháng 9 2021
Bài 3:
a: Ta có: \(6x\left(5x-3\right)+3x\left(1-10x\right)=7\)
\(\Leftrightarrow30x^2-18x+3x-30x^2=7\)
\(\Leftrightarrow x=-\dfrac{7}{15}\)
b: Ta có: \(3x\left(12x-4\right)-9x\left(4x-3\right)=30\)
\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)
hay x=2
c: ta có: \(x\left(5-2x\right)-2x\cdot\left(x-1\right)=15\)
\(\Leftrightarrow5x-2x^2-2x^2+2x-15=0\)
\(\Leftrightarrow-4x^2+7x-15=0\)
\(\text{Δ}=7^2-4\cdot\left(-4\right)\cdot\left(-15\right)=-191\)
Vì Δ<0 nên phương trình vô nghiệm
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
T
1
25 tháng 2 2023
b: ĐKXD: x<>1/5; x<>3
PT\(\Leftrightarrow\dfrac{3}{5x-1}-\dfrac{2}{x-3}=\dfrac{-4}{\left(5x-1\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
a: ĐKXĐ: x<>2/3; x<>-2/3
\(PT\Leftrightarrow\left(3x+2\right)^2-6\left(3x-2\right)=9x\)
=>9x^2+12x+4-18x+12-9x=0
=>9x^2-15x+16=0
=>\(x\in\varnothing\)
c: ĐKXĐ: x<>1/4; x<>-1/4
PT =>-3(4x+1)=2(4x-1)-6x-8
=>-12x-3=8x-2-6x-8
=>-12x-3=2x-10
=>-14x=-7
=>x=1/2
d: ĐKXĐ: x<>0; x<>2
\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>2(5-x)+7(x-2)=4(x-1)+x
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đung)
Vậy: S=R\{0;2}
e: DKXĐ: x<>0
PT \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
=>x(x^3+1-x^3+1)=3
=>2x=3
=>x=3/2
T
2
25 tháng 2 2023
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(ĐKXĐ:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{5\left(y-2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{\left(y-2\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2}{\left(y-2\right)\left(y+2\right)}-\dfrac{5y-10}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{y^2-4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Leftrightarrow\dfrac{y^2+y-2-5y+10-12-y^2+4}{\left(y-2\right)\left(y+2\right)}=0\)
\(\Rightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tm\right)\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\left(ĐKXĐ:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}+\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}-\dfrac{4}{\left(2z+3\right)^2}=0\)
\(⇔\dfrac{\left(2z+3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{3\left(2z-3\right)\left(2z+3\right)}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{4\left(2z-3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{12z^2-27}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{16z^2-48z+36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Leftrightarrow\dfrac{4z^2+12z+9+12z^2-27-16z^2+48z-36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)
\(\Rightarrow60z-54=0\)
\(\Leftrightarrow60z=54\)
\(\Leftrightarrow z=\dfrac{9}{10}\left(tm\right).\)
Y
25 tháng 2 2023
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(dkxd:y\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)-5\left(y-2\right)-12-y^2+4}{y^2-4}=0\)
\(\Leftrightarrow y^2+2y-y-2-5y+10-12-y^2+4=0\)
\(\Leftrightarrow-4y=0\)
\(\Leftrightarrow y=0\left(tmdk\right)\)
Vậy \(S=\left\{0\right\}\)
\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\)
\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}-\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}=\dfrac{4}{\left(2z+3\right)^2}\left(dkxd:z\ne\pm\dfrac{3}{2}\right)\)
\(\Leftrightarrow\left(2z+3\right)^2-3\left(4z^2-9\right)-4\left(2z-3\right)^2=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-4\left(4z^2-12z+9\right)=0\)
\(\Leftrightarrow4z^2+12z+9-12z^2+27-16z^2+48z-36=0\)
\(\Leftrightarrow-24z^2+60z=0\)
\(\Leftrightarrow-12z\left(2z-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-12z=0\\2z-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}z=0\left(tmdk\right)\\z=\dfrac{5}{2}\left(tmdk\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;\dfrac{5}{2}\right\}\)
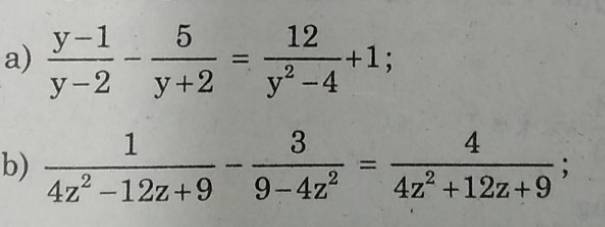
1: \(\dfrac{4x^3-2x^2-3x+1}{x-2}\)
\(=\dfrac{4x^3-8x^2+6x^2-12x+9x-18+19}{x-2}\)
\(=4x^2+6x+9+\dfrac{19}{x-2}\)
2: \(\dfrac{2x^4-x^3-3x^2-2x}{x-2}\)
\(=\dfrac{2x^4-4x^3+5x^3-10x^2+7x^2-14x+12x-24+24}{x-2}\)
\(=2x^3+5x^2+7x+12+\dfrac{24}{x-2}\)
còn cách giải nào khác ko bn cách giải này mik ko hiểu cho lắm