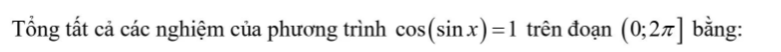K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
6 tháng 9 2021
Đặt \(y=sinx\left(y\in\left[-1;1\right]\right)\).
\(cos\left(sinx\right)=1\)
\(\Leftrightarrow cosy=1\)
\(\Leftrightarrow y=k2\pi\)
Vì \(y\in\left[-1;1\right]\Rightarrow-1\le k2\pi\le1\Leftrightarrow-\dfrac{1}{2\pi}\le k\le\dfrac{1}{2\pi}\)
\(\Rightarrow k=0\)
\(\Rightarrow y=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
\(\Leftrightarrow k\in\left\{0;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pi\\x=2\pi\end{matrix}\right.\)
\(\Rightarrow S=3\pi\)
KN
1
5 tháng 9 2017
pt<=>\(\left\{{}\begin{matrix}sin\left(3x+\dfrac{2\Pi}{3}\right)=sin\left(\dfrac{7\Pi}{4}-x\right)\\sin\left(3x+\dfrac{2\Pi}{3}\right)=-sin\left(\dfrac{7\Pi}{4}-x\right)=sin\left(x-\dfrac{7\Pi}{4}\right)\end{matrix}\right.\)
tới đây tự giải đi nhé!!!!
Kết quả:\(\left\{{}\begin{matrix}x=\dfrac{13\Pi}{48}+\dfrac{k\Pi}{2}\\x=\dfrac{-17\Pi}{24}+k\Pi\\x=\dfrac{-29\Pi}{24}+k\Pi\\x=\dfrac{25\Pi}{48}+\dfrac{k\Pi}{2}\end{matrix}\right.\)
DD
0
