
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{3}{1-\sqrt{2}}+\dfrac{\sqrt{2}-1}{\sqrt{2}+1}=\dfrac{3\left(\sqrt{2}+1\right)-\left(\sqrt{2}-1\right)^2}{-1}=-\left(3\sqrt{2}+3-3+2\sqrt{2}\right)=-5\sqrt{2}\)
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}+\dfrac{6}{1-\sqrt{5}}=\dfrac{\left(\sqrt{5}-1\right).\left(1-\sqrt{5}\right)+6.\left(\sqrt{5}+1\right)}{-4}=\dfrac{6-2\sqrt{5}-6\sqrt{5}-6}{4}=\dfrac{-8\sqrt{5}}{4}=-2\sqrt{5}\)
\(\dfrac{\sqrt{2}-\sqrt{3}}{2-\sqrt{6}}+\dfrac{\sqrt{3}-\sqrt{2}}{\sqrt{6}+2}=\dfrac{\left(\sqrt{2}-\sqrt{3}\right).\left(\sqrt{6}+2\right)+\left(\sqrt{3}-\sqrt{2}\right).\left(2-\sqrt{6}\right)}{-2}=\dfrac{2\left(\sqrt{12}-\sqrt{18}\right)}{-2}=\sqrt{18}-\sqrt{12}\)
\(\dfrac{-31+8\sqrt{x}-x}{x-8\sqrt{x}+15}-\dfrac{\sqrt{x}+5}{\sqrt{x}-3}-\dfrac{3\sqrt{x}-1}{5-\sqrt{x}}\)
\(=\dfrac{-31+8\sqrt{x}-x}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+5}{\sqrt{x}-3}+\dfrac{3\sqrt{x}-1}{\sqrt{x}-5}\)
\(=\dfrac{-31+8\sqrt{x}-x-x+25+3x-9\sqrt{x}-\sqrt{x}+3}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)

14, \(\frac{-7\sqrt{x}+7}{5\sqrt{x}-1}+\frac{2\sqrt{x}-2}{\sqrt{x}+2}+\frac{39\sqrt{x}+12}{5x+9\sqrt{x}-2}\)
\(=\frac{-7\sqrt{x}+7}{5\sqrt{x}-1}+\frac{2\sqrt{x}-2}{\sqrt{x}+2}+\frac{39\sqrt{x}+12}{\left(\sqrt{x}+2\right)\left(5\sqrt{x}-1\right)}\)
\(=\frac{\left(-7\sqrt{x}+7\right)\left(\sqrt{x}+2\right)+\left(2\sqrt{x}-2\right)\left(5\sqrt{x}-1\right)+39\sqrt{x}+12}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{-7x-14\sqrt{x}+7\sqrt{x}+14+10x-2\sqrt{x}-10\sqrt{x}+2+39\sqrt{x}+12}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{3x+20\sqrt{x}+28}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\left(3\sqrt{x}+14\right)\left(\sqrt{x}+2\right)}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{3\sqrt{x}+14}{5\sqrt{x}-1}\)

`16)(2sqrtx-4)/(3sqrtx-4)-(4+2sqrtx)/(sqrtx-2)+(x+13sqrtx-20)/(3x-10sqrtx+8)`
`=((2sqrtx-4)(sqrtx-2)-(4+2sqrtx)(3sqrtx-4)+x+13sqrtx-20)/((3sqrtx-4)(sqrtx-2)`
`=(2x-8sqrtx+8-6x-4sqrtx+16+x+13sqrtx-20)/((3sqrtx-4)(sqrtx-2)`
`=(-3x+sqrtx+4)/((3sqrtx-4)(sqrtx-2)`
`=(-(3sqrtx-4)(sqrtx+1))/((3sqrtx-4)(sqrtx-2)`
`=(-(sqrtx+1))/(sqrtx-2)`

`15)(-5sqrtx+4)/(3sqrtx-2)+(6sqrtx+4)/(2sqrtx+3)+(29sqrtx-28)/(3(6x+5sqrtx-6))`
`=(3(-5sqrtx+4)(2sqrtx+3)+3(6sqrtx+4)(3sqrtx-2)+29sqrtx-28)/(3(3sqrtx-2)(2sqrtx+3))`
`=(-30x-21sqrtx+36+54x-24+29sqrtx-28)/(3(3sqrtx-2)(2sqrtx+3))`
`=(24x+8sqrtx-16)/(3(3sqrtx-2)(2sqrtx+3))`
`=(8(3sqrtx-2)(sqrtx+1))/(3(3sqrtx-2)(2sqrtx+3))`
`=(8(sqrtx+1))/(3(2sqrtx+3))`

14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)

ĐKXĐ : \(\left\{{}\begin{matrix}x\ge0\\x\ne49\end{matrix}\right.\)
Ta có : \(\dfrac{7\sqrt{x}-1}{\sqrt{x}-7}-\dfrac{6\sqrt{x}+1}{\sqrt{x}+1}+\dfrac{1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(7\sqrt{x}-1\right)-\left(\sqrt{x}-7\right)\left(6\sqrt{x}+1\right)+1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{7x+7\sqrt{x}-\sqrt{x}-1-\left(6x-42\sqrt{x}+\sqrt{x}-7\right)+1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{7x+7\sqrt{x}-\sqrt{x}-1-6x+42\sqrt{x}-\sqrt{x}+7+1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-8\sqrt{x}+7}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-7\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
19) Ta có: \(\dfrac{7\sqrt{x}-1}{\sqrt{x}-7}-\dfrac{6\sqrt{x}+1}{\sqrt{x}+1}+\dfrac{1-55\sqrt{x}}{x-6\sqrt{x}-7}\)
\(=\dfrac{\left(7\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(6\sqrt{x}+1\right)\left(\sqrt{x}-7\right)}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}+\dfrac{1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{7x+7\sqrt{x}-\sqrt{x}-1-6x+42\sqrt{x}-\sqrt{x}+7+1-55\sqrt{x}}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-8\sqrt{x}+7}{\left(\sqrt{x}-7\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

11.
\(=\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{x-9}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}-2}{3+\sqrt{x}}\)
12.
\(=\frac{(3-\sqrt{x})(3\sqrt{x}-2)+(5\sqrt{x}+7)(3\sqrt{x}+4)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+52\sqrt{x}+22}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+10\sqrt{x}-12}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(3\sqrt{x}-2)(2\sqrt{x}+3)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(2\sqrt{x}+3)}{5\sqrt{x}+7}\)

80)
a)
\(\left(2-\sqrt{2}\right)\left(-5\sqrt{2}\right)-\left(3\sqrt{2}-5\right)^2\)
\(=-10\sqrt{2}+5.2-\left(18-30\sqrt{2}+25\right)\)
Đáp số : \(-33+20\sqrt{2}\)
b)
\(2\sqrt{3a}-\sqrt{75a}+a\sqrt{\frac{13,5}{2a}}-\frac{2}{5}\sqrt{300a^3}\)
\(=2\sqrt{3a}-5\sqrt{3a}+\frac{a}{2a}\sqrt{27a}-\frac{2}{5}.10a\sqrt{3a}\)
Đáp số : \(-\left(1,5+4a\right)\sqrt{3a}\)
81)
a) Ta có : \(\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2+\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{a+2\sqrt{ab}+b+a-2\sqrt{ab}+b}{a-b}\)
\(=\frac{2\left(a+b\right)}{a-b}\)( Với \(a\ge0\); \(b\ge0\)và \(a\ne b\))
b) Ta có : \(\frac{a-b}{\sqrt{a}-\sqrt{b}}+\frac{\sqrt{a^3}-\sqrt{b^3}}{a-b}=\frac{\left(a-b\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}\right)^2+\left(\sqrt{b}\right)^2}-\frac{a\sqrt{a}-b\sqrt{b}}{a-b}\)
\(=\frac{a\sqrt{a}+a\sqrt{b}-b\sqrt{a}-b\sqrt{b}}{a-b}-\frac{a\sqrt{a}-b\sqrt{b}}{a-b}\)
\(=\frac{a\sqrt{b}-b\sqrt{a}}{a-b}\)( Với \(a\ge b\); \(b\ge0\)và \(a\ne b\))

=9.887666677000000000000
Toi mat 12 phut de tinh do nha nen ban phai k tui nha
 giải giúp bài 14 15 16 17 của bài 14
giải giúp bài 14 15 16 17 của bài 14  giải giúp em bài 14 15 16 17 của bài 14 nha
giải giúp em bài 14 15 16 17 của bài 14 nha giải giúp em bài 14 15 16 17 của bài 14 nha
giải giúp em bài 14 15 16 17 của bài 14 nha giải giúp câu 16 của bài 14 i
giải giúp câu 16 của bài 14 i Giải giúp câu 15 của bài 14 i
Giải giúp câu 15 của bài 14 i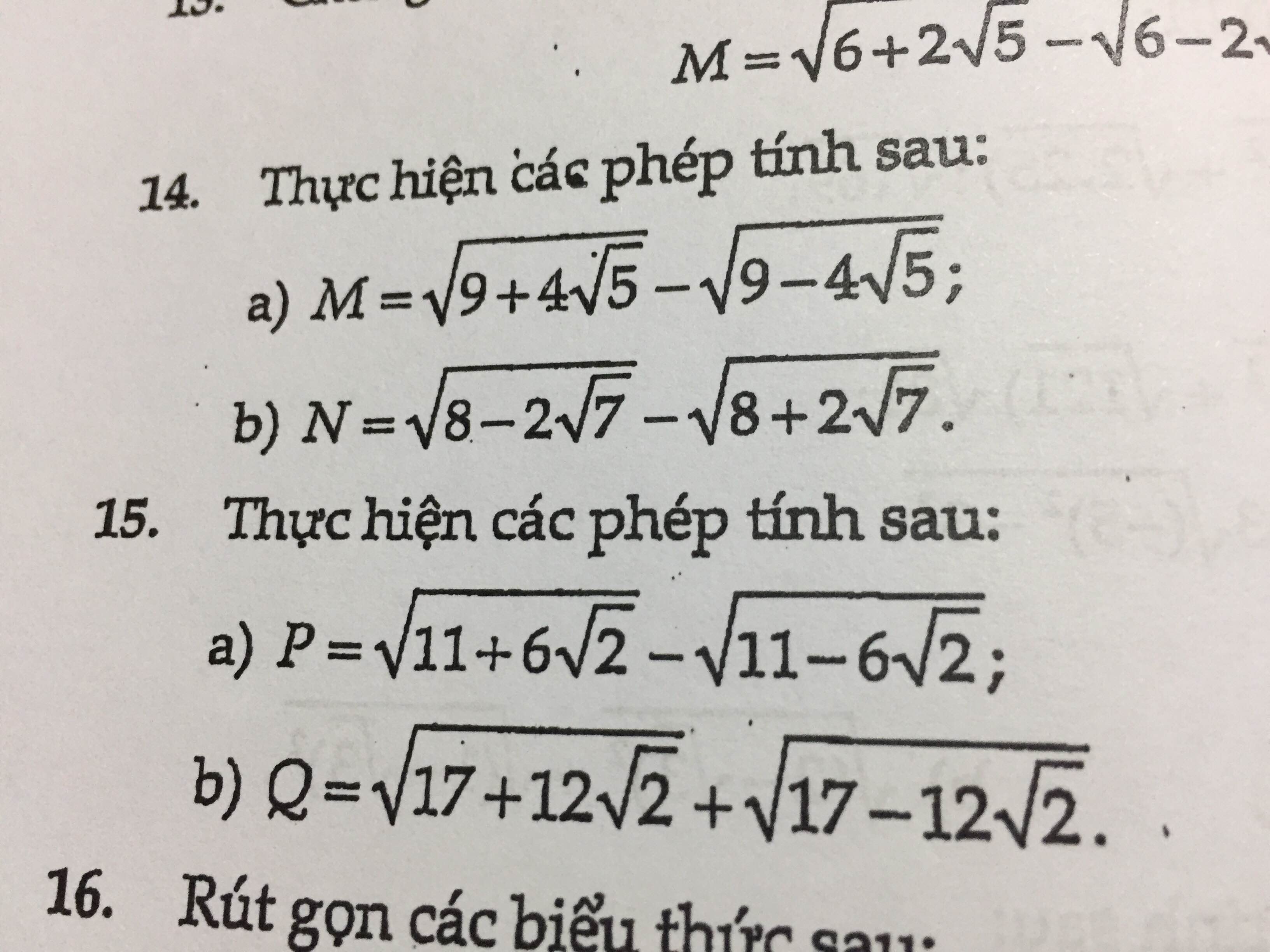
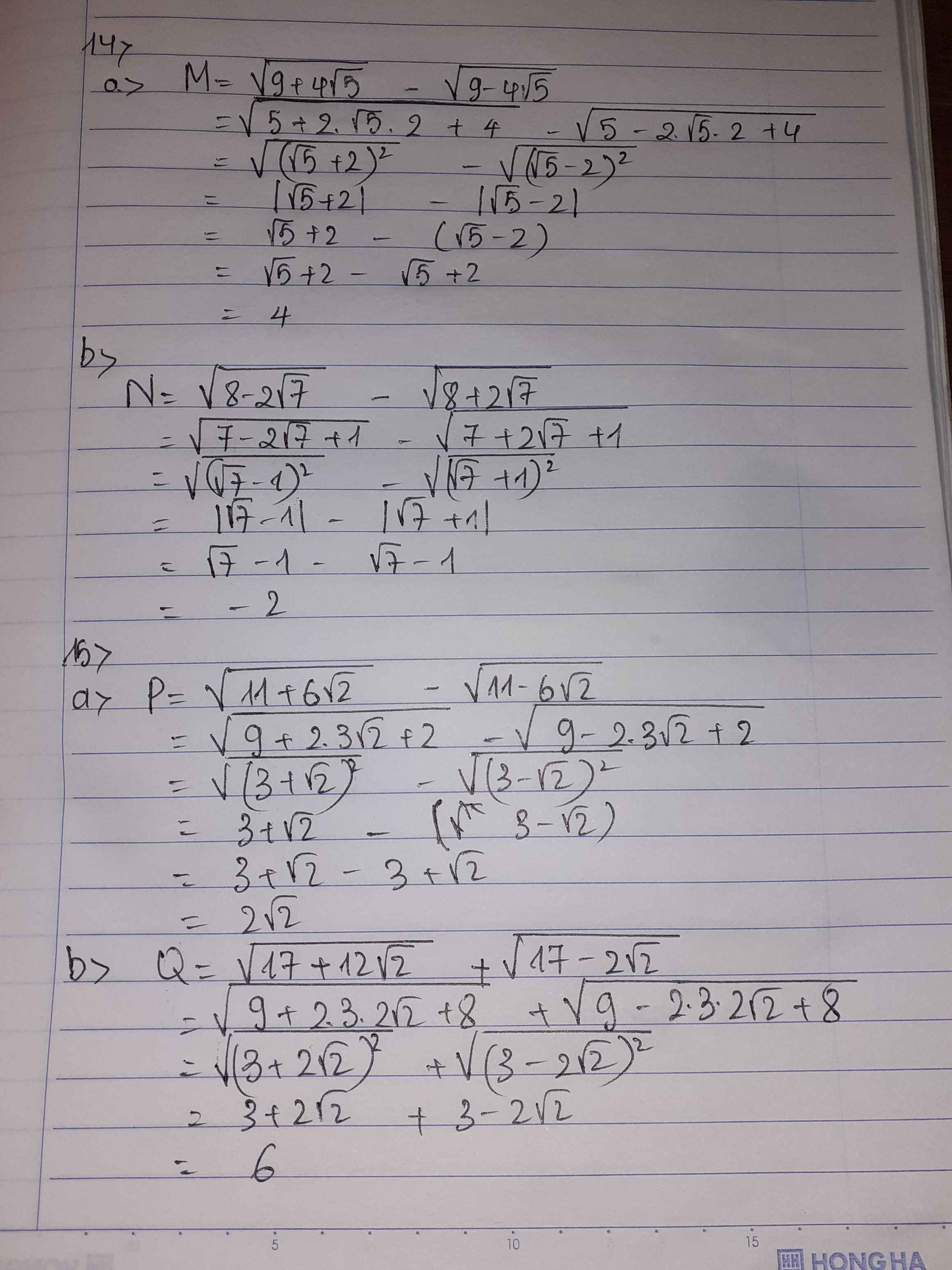
 giải giúp bài 19 của bài 14 i
giải giúp bài 19 của bài 14 i giải giúp em bài 11 12 13 của bài 14 đi ạ
giải giúp em bài 11 12 13 của bài 14 đi ạ
16. \(\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}-\dfrac{4+2\sqrt{x}}{\sqrt{x}-2}+\dfrac{x+13\sqrt{x}-20}{3x-10\sqrt{x}+8}\)
=\(\dfrac{\left(2\sqrt{x}-4\right)\left(\sqrt{x}-2\right)-\left(4+2\sqrt{x}\right)\left(3\sqrt{x}-4\right)+x+13\sqrt{x}-20}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
=\(\dfrac{2x-8\sqrt{x}+8-\left(4\sqrt{x}+6x-16\right)+x+13\sqrt{x}-20}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
=\(\dfrac{2x-8\sqrt{x}+8-4\sqrt{x}-6x+16+x+13\sqrt{x}-20}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
=\(\dfrac{-3x+\sqrt{x}+4}{\left(3\sqrt{x}-4\right)\left(x+2\right)}\)
=\(\dfrac{-\left(3x+3\sqrt{x}-4\sqrt{x}-4\right)}{\left(3\sqrt{x}-4\right)\left(x+2\right)}\)
=\(\dfrac{-\left(3\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}+2\right)}\)=\(\dfrac{-\sqrt{x}-1}{\sqrt{x}+2}\)
14.
=\(\dfrac{-\left(7\sqrt{x}+7\right)\left(\sqrt{x}+2\right)}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)+\(\dfrac{\left(2\sqrt{x}-2\right)\left(5\sqrt{x}-1\right)}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)+\(\dfrac{39\sqrt{x}+12}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{-7x-21\sqrt{x}-14}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)+\(\dfrac{10x-12\sqrt{x}+2}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)+\(\dfrac{39\sqrt{x}+12}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{-7x-21\sqrt{x}-14+10x-12\sqrt{x}+2+39\sqrt{x}+12}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{3x-6\sqrt{x}}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)=\(\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(5\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
17.