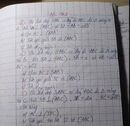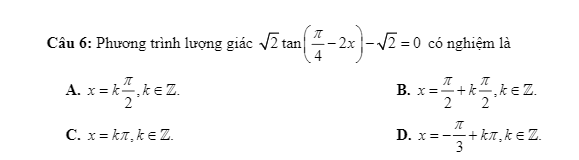DL
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
Số hạng đó là số hạng thứ 4 \(\Rightarrow k=3\) nên có dạng:
\(C_6^3\left(2x\right)^3.\left(-y^2\right)^3=-C_6^3\left(2x\right)^3y^6\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
a.
Kéo dài AB và DC cắt nhau tại E
Trong mp (SCD), nối EM kéo dài cắt SD tại F
\(\Rightarrow\) Tứ giác ABMF là thiết diện của (BAM) và chóp
b.
Trong mp (SCD), nối MN kéo dài cắt SE tại P ( điểm E được dựng ở câu a)
Trong mp (SAB), nối AP cắt SB tại Q
\(\Rightarrow\) Tứ giác ANMQ là thiết diện của (MAN) và chóp
18 tháng 6 2021
3)\(sin6x.sin2x=sin5x.sinx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x-cos8x\right)=\dfrac{1}{2}\left(cos4x-cos6x\right)\)
\(\Leftrightarrow cos8x=cos6x\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=6x+k2\pi\\8x=-6x+k2\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{7}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
13)\(cosx.cos3x-sin2x.sin6x-sin4x.sin6x=0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(cos2x+cos4x\right)-\dfrac{1}{2}\left(cos4x-cos8x\right)-\dfrac{1}{2}\left(cos2x-cos10x\right)=0\)
\(\Leftrightarrow cos8x+cos10x=0\)
\(\Leftrightarrow2.cos9x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos9x=0\\cosx=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{k\pi}{9}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2020
\(sin2x+\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=m+2\)
\(\Leftrightarrow2sinx.cosx+sinx+cosx=m+2\)
Đặt \(sinx+cosx=t\) \(\left(0< t\le\sqrt{2}\right)\)
\(\Rightarrow2sinx.cosx=t^2-1\)
Pt trở thành:
\(t^2-1+t=m+2\Leftrightarrow t^2+t-3=m\) (1)
Dựa vào đường tròn lượng giác, để pt có đúng 2 nghiệm thuộc khoảng đã cho \(\Leftrightarrow\left(1\right)\) có 2 nghiệm thuộc \(\left(0;\frac{\sqrt{2}}{2}\right)\), hoặc \(\left(1\right)\) có nghiệm kép thuộc \(\left(\frac{\sqrt{2}}{2};1\right)\); hoặc (1) có 2 nghiệm thỏa mãn \(t_2< 0< \frac{\sqrt{2}}{2}\le t_1< 1\) hoặc (1) có 2 nghiệm phân biệt, trong đó \(\left\{{}\begin{matrix}t_1=1\\0< t_2< \frac{\sqrt{2}}{2}\end{matrix}\right.\)
Dựa vào đồ thị parabol, bạn tự biện luận nốt, nhiều trường hợp quá nhìn ngán vô cùng :D
NM
2
HP
20 tháng 8 2021
\(tanx=-tan\dfrac{\pi}{5}\)
\(\Leftrightarrow tanx=tan\left(-\dfrac{\pi}{5}\right)\)
\(\Leftrightarrow x=-\dfrac{\pi}{5}+k\pi\)
NM
20 tháng 8 2021
Mình quên mất, nó nằm trong khoảng (π/2; π) nha, mình xin lỗi
