K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
2
H
4 tháng 4 2021
Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
4 tháng 4 2021
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm
NT
1
AH
Akai Haruma
Giáo viên
23 tháng 12 2022
Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)
MN
3 tháng 7 2021
\(6-\sqrt{17}=\sqrt{36}-\sqrt{17}\)
Với :
\(\sqrt{36}-\sqrt{17}>\sqrt{31}-\sqrt{17}\)
Mặt khác :
\(\sqrt{31}-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
Nên :
\(6-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
3 tháng 7 2021
Cách khác:
Ta có: \(\left(\sqrt{31}-\sqrt{19}\right)^2=50-2\sqrt{589}\)
\(\left(6-\sqrt{17}\right)^2=53-12\sqrt{17}=50+3-12\sqrt{17}\)
mà \(-2\sqrt{589}< 3-12\sqrt{17}\)
nên \(\sqrt{31}-\sqrt{19}>6-\sqrt{17}\)
CH
giải giúp mình bài nay bằng máy tính casio hộ mình nha(nhớ giải chi tiết hộ mình)
tính: \(1023456^3\)
6
NM
1
TK
1
3 tháng 7 2021
a, \(\sqrt{15}+\sqrt{8}< \sqrt{16}+\sqrt{9}=4+3=7\)
\(\Rightarrow\sqrt{15}+\sqrt{8}< 7\)
b, \(\sqrt{10}+\sqrt{17}+1>\sqrt{9}+\sqrt{16}+1=3+4+1=8\)
\(\sqrt{61}< \sqrt{64}=8\)
\(\Rightarrow\sqrt{10}+\sqrt{17}+1>\sqrt{61}\)
c, \(\sqrt{10}+\sqrt{5}+1>\sqrt{9}+\sqrt{4}+1=3+2+1=6\)
\(\sqrt{35}< \sqrt{36}=6\)
\(\Rightarrow\sqrt{10}+\sqrt{5}+1>\sqrt{35}\)
QA
1
TT
2
KT
14 tháng 4 2018
Nếu: \(x-1\ge0\) \(\Leftrightarrow\)\(x\ge1\) thì: \(\left|x-1\right|=x-1\)
Khi đó ta có: \(x^2-3x+2+x-1=0\)
\(\Leftrightarrow\) \(\left(x-1\right)^2=0\)
\(\Leftrightarrow\) \(x-1=0\)
\(\Leftrightarrow\) \(x=1\) (thỏa mãn)
Nếu \(x-1< 0\)\(\Leftrightarrow\)\(x< 1\) thì \(\left|x-1\right|=1-x\)
Khi đó ta có: \(x^2-3x+2+1-x=0\)
\(\Leftrightarrow\) \(x^2-4x+3=0\)
\(\Leftrightarrow\) \(\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\) \(\orbr{\begin{cases}x-1=0\\x-3=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\\x=3\end{cases}}\) (không thỏa mãn)
Vậy....
14 tháng 4 2018
Lập bảng xét dấu :
| x | 1 | ||
| x-1 | - | 0 | + |
+) Nếu \(x\ge1\Leftrightarrow|x-1|=x-1\)
\(pt\Leftrightarrow x^2-3x+2+\left(x-1\right)=0\)
\(\Leftrightarrow x^2-3x+2+x-1=0\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\left(tm\right)\)
+) Nếu \(x< 1\Leftrightarrow|x-1|=1-x\)
\(pt\Leftrightarrow x^2-3x+2+\left(1-x\right)=0\)
\(\Leftrightarrow x^2-3x+2+1-x=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow\left(x^2-4x+4\right)-1=0\)
\(\Leftrightarrow\left(x-2\right)^2=1\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=-\sqrt{1}\\x-2=\sqrt{1}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x-2=-1\\x-2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=3\end{cases}}\) ( loại )
Vậy phương trình có tập nghiệm \(S=\left\{1\right\}\)
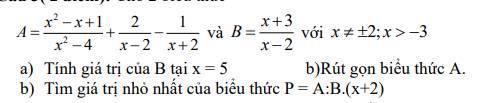
b: \(=x^3-3x-5x^2+15-x^3+8=-5x^2-3x+23\)