NH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2
H
26 tháng 12 2022
Giải :
\(\dfrac{x+11}{89}+\dfrac{x+13}{87}-\dfrac{x+15}{85}-\dfrac{x+17}{83}=0\\ =>\left(\dfrac{x+11}{89}+1\right)+\left(\dfrac{x+13}{87}+1\right)-\left(\dfrac{x+15}{85}+1\right)-\left(\dfrac{x+17}{83}+1\right)=0\\ =>\left(\dfrac{x+11+89}{89}\right)+\dfrac{x+13+87}{87}-\dfrac{x+15+85}{85}-\dfrac{x+17+83}{83}=0\\ =>\dfrac{x+100}{89}+\dfrac{x+100}{87}-\dfrac{x+100}{85}-\dfrac{x+100}{83}=0\\ =>\left(x+100\right)\left(\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}\right)=0\\ =>\left[{}\begin{matrix}x+100=0\\\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}=0\left(voli\right)\end{matrix}\right.=>x=-100\)
NH
1
NH
2
H
26 tháng 12 2022
\(2x=3y\\ =>\dfrac{x}{3}=\dfrac{y}{2}\\ 4y=5z\\ =>\dfrac{y}{5}=\dfrac{z}{4}\\ \dfrac{x}{3}=\dfrac{y}{2}\\ =>\dfrac{x}{3.5}=\dfrac{y}{2.5}\\ =>\dfrac{x}{15}=\dfrac{y}{10}\\ \dfrac{y}{5}=\dfrac{z}{4}\\ =>\dfrac{y}{5.2}=\dfrac{z}{4.2}\\ =>\dfrac{y}{10}=\dfrac{z}{8}\\ =>\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}=\dfrac{x+y+z}{15+10+8}=\dfrac{11}{33}=\dfrac{1}{3}\\ =>\left\{{}\begin{matrix}x=\dfrac{1}{3}.15=5\\y=\dfrac{1}{3}.10=\dfrac{10}{3}\\z=\dfrac{1}{3}.8=\dfrac{8}{3}\end{matrix}\right.\)
NH
2
NH
2
H
26 tháng 12 2022
\(a,\dfrac{3^{10}.11+9^5.5}{27^3.2^4}.x=-9\\ =>\dfrac{3^{10}.11+\left(3^2\right)^5.5}{\left(3^3\right)^3.2^4}.x=-9\\ =>\dfrac{3^{10}.\left(11+5\right)}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.16}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.2^4}{3^9.2^4}.x=-9\\ =>3^1.x=-9\\ =>x=-9:3\\ =>x=-3\)
NH
2
H
26 tháng 12 2022
Giải
\(\sqrt{\dfrac{9}{4}}-\left|2x+1\right|=0,75\)
TH1: \(\left|2x+1\right|=2x+1\)
\(=>\sqrt{\dfrac{9}{4}}-\left(2x+1\right)=0,75\\ =>\dfrac{3}{2}-2x-1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}-1\right)-2x=\dfrac{3}{4}\\ =>\dfrac{1}{2}-2x=\dfrac{3}{4}\\ =>2x=\dfrac{1}{2}-\dfrac{3}{4}\\ =>2x=-\dfrac{1}{4}\\ =>x=\left(-\dfrac{1}{4}\right):2\\ =>x=-\dfrac{1}{8}\)
\(TH2:\left|2x+1\right|=-2x-1\\ =>\sqrt{\dfrac{9}{4}}-\left(-2x-1\right)=\dfrac{3}{4}\\ =>\dfrac{3}{2}+2x+1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}+1\right)+2x=\dfrac{3}{4}\\ =>\dfrac{5}{2}+2x=\dfrac{3}{4}\\ =>2x=\dfrac{3}{4}-\dfrac{5}{2}\\ =>2x=-\dfrac{7}{4}\\ =>x=\left(-\dfrac{7}{4}\right):2\\ =>x=-\dfrac{7}{8}\)
NH
2
H
26 tháng 12 2022
Giải
\(a,5-\left(x-2\right)^2=-4\\ =>\left(x-2\right)^2=5-\left(-4\right)\\ =>\left(x-2\right)^2=9\\ =>\left[{}\begin{matrix}\left(x-2\right)^2=3^2\\\left(x-2\right)^2=\left(-3\right)^2\end{matrix}\right.=>\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.=>\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy \(x=5;x=-1\)
NH
2
H
26 tháng 12 2022
Giải
\(đk:6x-2\ne0=>x\ne\dfrac{1}{3}\\\dfrac{x+2}{6x-2}=\dfrac{1}{4}\\ =>\dfrac{4\left(x+2\right)}{4\left(6x-2\right)}=\dfrac{6x-2}{4\left(6x-2\right)}\\ =>4\left(x+2\right)=6x-2\\ =>4x+8-6x+2=0\\ =>-2x+10=0\\ =>-2x=-10\\ =>x=\left(-10\right):\left(-2\right)\\ =>x=5\left(thoamanđk\right)\)
Vậy \(x=5\)
NH
1
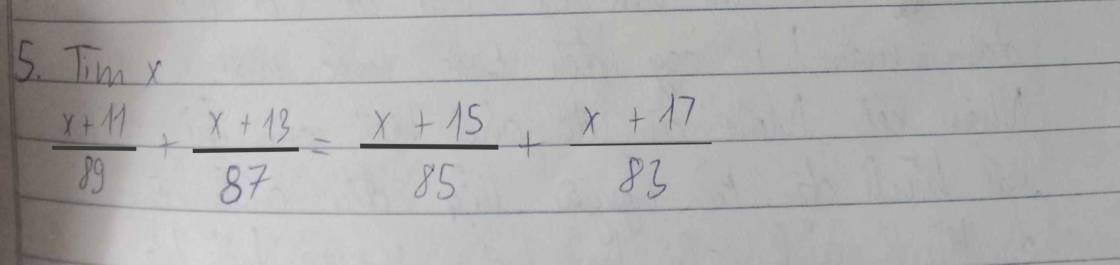
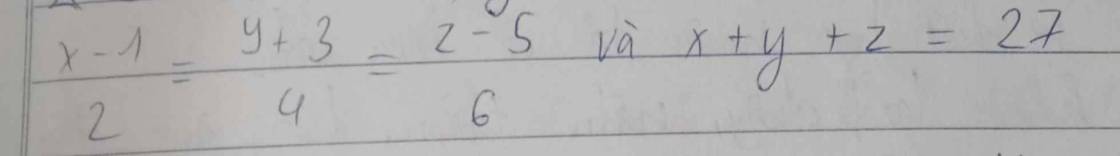
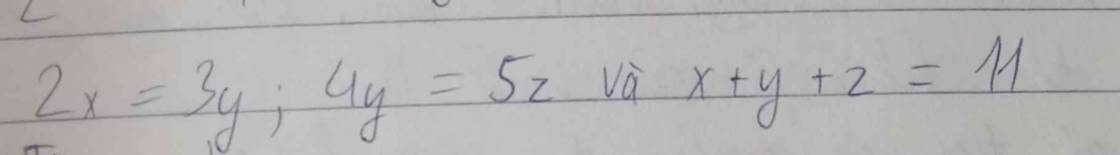
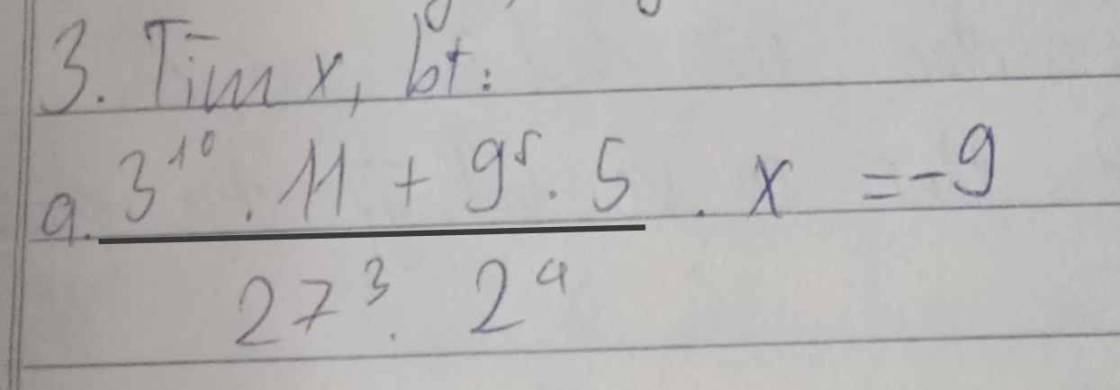
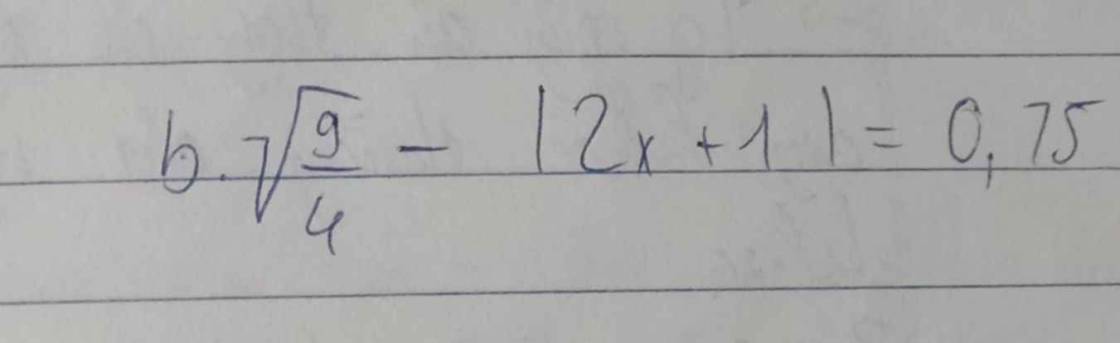
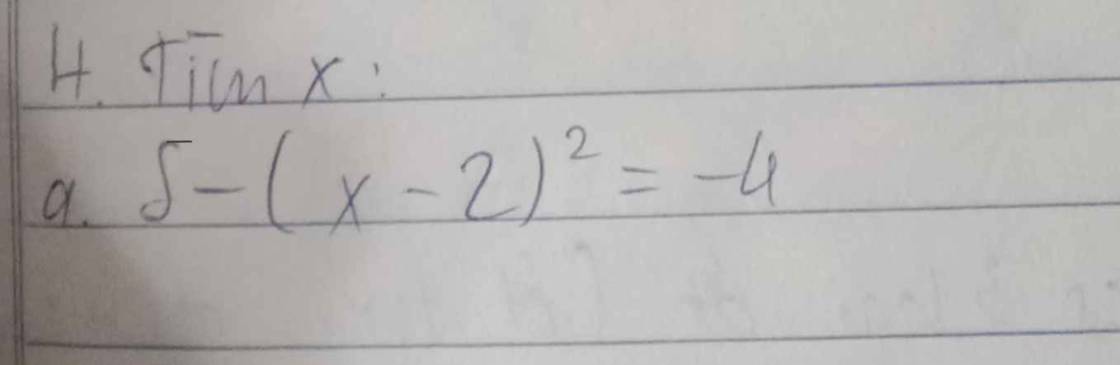
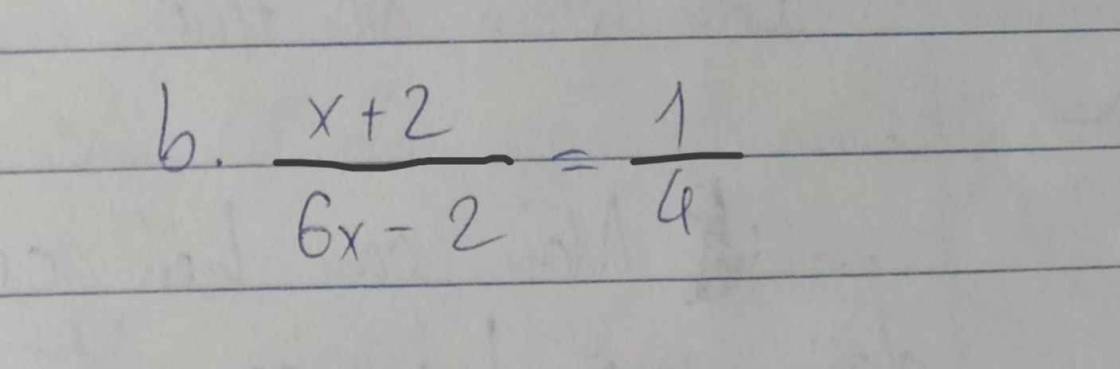
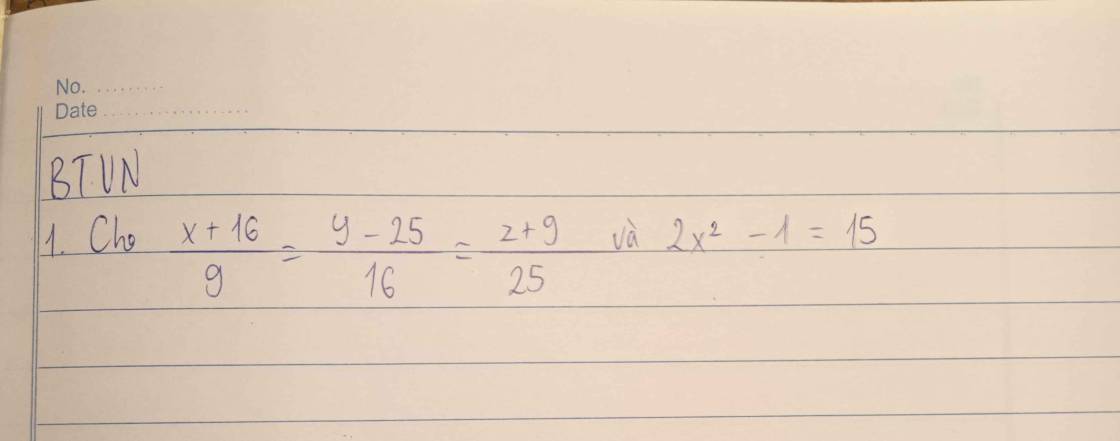
Giải
\(\dfrac{x}{3}=\dfrac{y}{4}\\ \Leftrightarrow\dfrac{x}{3.3}=\dfrac{y}{4.3}\\\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12}\\ \dfrac{y}{3}=\dfrac{z}{5}\\ \Leftrightarrow \dfrac{y}{3.4}=\dfrac{z}{5.4}\\ \Leftrightarrow\dfrac{y}{12}=\dfrac{z}{20}\\ =>\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x+3x+z}{2.9+3.12+20}=\dfrac{6}{74}=\dfrac{3}{37}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{37}\times9=\dfrac{27}{37}\\y=\dfrac{3}{37}\times12=\dfrac{36}{37}\\z=\dfrac{3}{37}\times20=\dfrac{60}{37}\end{matrix}\right.\)