K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 10 2021
Câu 1:
\(x^2\left(x^2-y^2\right)+\left(x^2+y^2\right)y^2=x^4-x^2y^2+x^2y^2+y^4=x^4+y^4\)
=> Chọn C
Câu 2:
\(3x^2y\left(2x^2y^2-5xy\right)=6x^4y^3-15x^3y^2\)
=> Chọn B
Câu 3:
\(x^3-6x^2+12x-8=\left(x-2\right)^3=\left(-2-2\right)^3=\left(-4\right)^3=-64\)
=> Chọn A
Câu 4:
\(\left(a+b\right)^2-4ab=a^2+b^2+2ab-4ab=a^2-2ab+b^2=\left(a-b\right)^2\)
=> Chọn B
Câu 5:
\(9x^2+30x+25=\left(3x+5\right)^2\)
=> Chọn C
NN
1
DT
10 tháng 11 2021
hai bài câu a mik lm đc r nhe mn lm giúp mik câu b thôi ạ mik ko bt lm;-;
10 tháng 11 2021
Bài 3:
\(a,=-\left(x^2-2x+1\right)-2=-\left(x-1\right)^2-2\le-2\)
Dấu \("="\Leftrightarrow x=1\)
\(b,=-2\left(x^2+2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)+\dfrac{9}{8}=-2\left(x+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\le\dfrac{9}{8}\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{4}\)
Bài 4:
\(a,=\left(x^2+2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{21}{4}=\left(x+\dfrac{5}{2}\right)^2-\dfrac{21}{4}\ge-\dfrac{21}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{5}{2}\)
\(b,=\left(x^2-8x+16\right)+1=\left(x-4\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x=4\)
XD
2
28 tháng 10 2021
2
a) \(=x\left(3x^3-x^2+5\right)\)
b) \(=\left(2x+3y\right)\left(x-y\right)\)
c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)
LN
28 tháng 10 2021
a, = x.(3x3 - x2 + 5)
b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)
c, = x2 - 3x - 4x + 12 = (x2 - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)
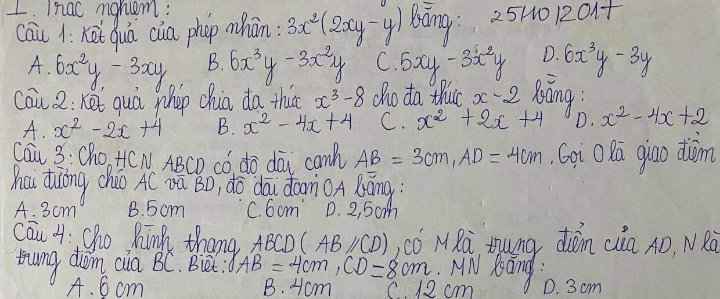
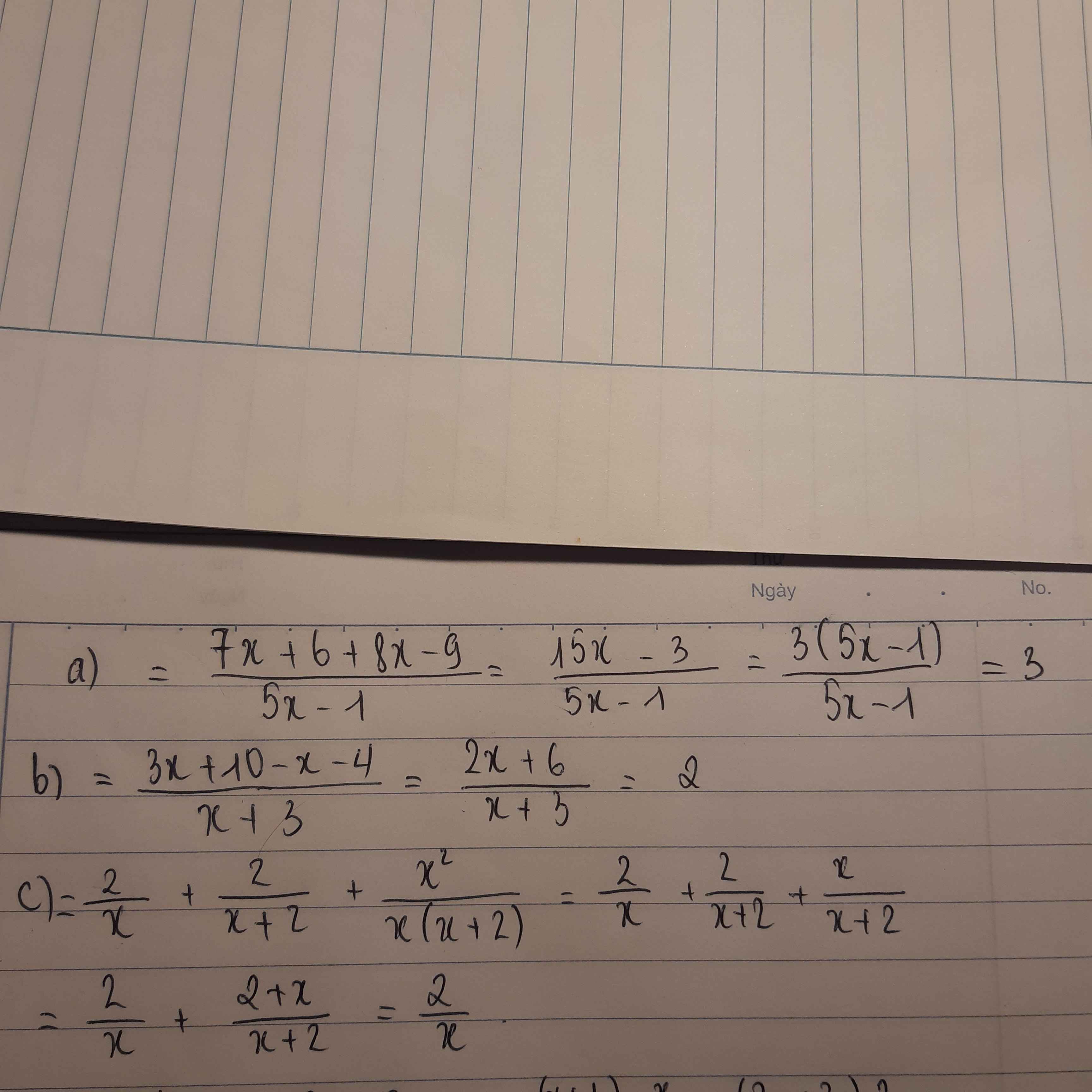
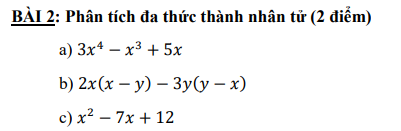
Câu 1: B
Câu 2: A
Câu 3: D
Câu 4: A